Ảnh hưởng khối lượng đầu búa đến ứng suất cực đại khi đóng cọc bê tông trong nền đồng nhất đáy tựa trên nền cứng

 1 
ảnh hưởng khối lượng đầu búa đến ứng suất cực đại khi đóng cọc 
bê tông trong nền đồng nhất đáy tựa trên nền cứng 
NCS Bùi quang nhung - Trường đại học thuỷ lợi 
I.Đặt vấn đề 
 Trên cơ sở lý thuyết va chạm của vật rắn vào thanh đàn hồi [1],[2] & [3] một số tác giả đã 
tính được độ bền của cọc bằng cách chọn đệm đầu cọc. Trong [4] các tác giả đã xét ảnh hưởng 
khối lượng đầu búa, đệm đầu cọc... đến lực nén của đệm đàn hồi lên đầu cọc đóng trong nền 
đồng nhất hai lớp đáy cọc gặp lực chống không đổi. Nội dung bài báo này sẽ khảo sát ảnh 
hưởng khối lượng đầu búa đến ứng suất nén cực đại tại đáy cọc khi cọc đóng trong nền đồng 
nhất đáy cọc tựa trên cứng. 
II. Thiết lập Bài toán. 
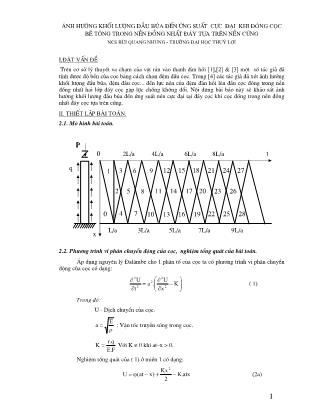
2.1. Mô hình bài toán. 
2.2. Phương trình vi phân chuyển động của cọc, nghiệm tổng quát của bài toán. 
áp dụng nguyên lý Đalămbe cho 1 phân tố của cọc ta có phương trình vi phân chuyển 
động của cọc có dạng: 




K
x
U
.a
t
U
2
2
2
2
2
 ( 1) 
Trong đó: 
U - Dịch chuyển của cọc. 
E
a : Vận tốc truyền sóng trong cọc. 
F.E
q.r
K Với K 0 khi at–x > 0. 
Nghiệm tổng quát của ( 1) ở miền 1 có dạng: 
 atx.K
2
Kx
)xat(U
2
 (2a) 
P 
 0 2L/a 4L/a 6L/a 8L/a 
 L/a 3L/a 5L/a 7L/a 9L/a 
1 
2 
4 
3 
5 
7 
6 
8 
10 
9 
11 
13 
12 
14 
16 
15 
17 
19 
18 
20 
22 
21 
0 
q 
t 
x 
23 
25 
24 
26 
28 
27 
 2 
Nghiệm tổng quát của ( 1) ở miền 2,3 có dạng: 
 2)xL(
2
K
)xat(U (2b) 
Nghiệm tổng quát của (1) các miền còn lại có dạng: 
 2)xL(
2
K
)xat()xat(U  (2c) 
2.3. Điều kiện của bài toán. 
a. Điều kiện đầu. 
Ta chọn thời điểm ban đầu t = 0 trùng với thời điểm bắt đầu va chạm thì: 
 ;0;0 


x
U
U (3) 
b. Điều kiện biên. 
Tại x = 0 
FE
tP
x
U
.
)(


 ( 4a) 
Tại x = L 
 0
t
U


 (4b) 
III. trạng thái ứng suất của cọc trong khi đóng. 
 Theo [ 3] ta có ứng suất trong cọc ở miền 1 là : 
   )
a
x
t(P
F
1
)xat(K)xat(E 0
'
11  
 ứng suất trong cọc ở miền 2: 
  )Lat(EK)
a
x
t(P
F
1
)xL(K)xat('E 02  
 ứng suất trong cọc ở miền 3 : 
   x.K.E)
a
x
t(P
F
1
)xL(K)xat('E 13  
 ứng suất trong cọc ở miền còn lại được tính theo công thức : 
  )xL(K)xat(')xat('E   
 ứng suất trong cọc ở miền 4: 
)32(.)
2
()(
1
004 LxatKE
a
xL
tP
a
x
tP
F
  
 ứng suất trong cọc ở miền 5 là : 
)22(.)
2
()(
1
015 LxatKE
a
xL
tP
a
x
tP
F
  
 ứng suất trong cọc tại miền 6 là : 
 3 
KxE
a
Lx
tP
a
x
tP
a
Lx
tP
F
.3
221
0206 
  
 ứng suất trong cọc ở miền 7 là: 
)(.
21
117 xLKE
a
Lx
tP
a
x
tP
F
  
 ứng suất trong cọc ở miền 8 là : 
[ )32(.
221
1028 LxatKE
a
Lx
tP
a
Lx
tP
a
x
tP
F
  
 ứng suất trong cọc ở miền 10 là : 
)L7xat2(K.E
a
L4x
tP
a
L2x
tP
a
L2x
tP
a
x
tP
F
1
020210 
 
 ứng suất trong cọc ở miền 9 là : 
EKx
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
F
4221
02319 
 ứng suất trong cọc ở miền 11 là : 
)4(
4221
023111 LatEK
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
F
  
 ứng suất trong cọc ở miền 13 là : 
)(
2421
313113 xLEK
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
F
  
 ứng suất trong cọc ở miền 12 là: 
EKx
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
a
Lx
tP
F
42
421
024
0212
 ứng suất trong cọc ở miền 14 là : 
)5(
24
421
314
0214
LatEK
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
a
Lx
tP
F
 
 ứng suất trong cọc ở miền 16 là : 
 4 
)112(
64
2421
02
402416
LxatEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 ứng suất trong cọc ở miền 17 là: 
)62(
64
2241
02
453117
LxatEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
a
Lx
tP
a
Lx
tP
F

 ứng suất trong cọc ở miền 19 là : 
)(
246
421
531
13519
LxEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 ứng suất trong cọc ở miền 18là : 
EKx
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
3
642
6:421
024
024618
 
 ứng suất trong cọc ở miền 20 là : 
)72(
642
6:421
135
024620
LxatEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 ứng suất trong cọc ở miền 22 là: 
)152(
8642
6:421
0246
024622
LxatEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 ứng suất trong cọc ở miền 21 là : 
EKx
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
642
6:421
135
135721
ứng suất trong cọc ở miền 23 là : 
 5 
)8(
8642
6:421
0246
135723
LatEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 ứng suất trong cọc ở miền 25 là: 
)(
8642
6:421
1357
135725
xLEK
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
Lx
tP
a
x
tP
F
 
 Nếu va chạm chưa kết thúc trong khoảng thời gian 
a
L
t
a
L 87
 , lí luận tương tự như trên 
xác định được ứng suất trong cọc ở các miền còn lại. 
Iv. tính toán cụ thể 
 Dựa vào công thức giải tích xác định trạng thái ứng suất của cọc với chương trình máy 
tính ngôn ngữ lập trình Pascal, chúng ta xác định ảnh hưởng khối lượng đầu búa đến thời gian 
va chạm và ứng suất nén cực đại tại đáy cọc. 
 Cọc đóng trong nền đồng nhất đáy cọc tựa trên nền cứng. 
 Lực ma sát mặt bên phân bố đều q= 1.5 N/cm2 . 
 Cọc bê tông cốt thép Mác 300 có kích thước 35x 35 x 1400 (cm). 
 Môđun đàn hồi E = 3.11 x 106 (N/cm2). 
 ứng suất nén cho phép []n = 1750 (N/cm
2). 
 Khối lượng riêng của cọc = 0.0024 (kg/cm3). 
 Chọn đầu búa có khối lượng: M1 = 2100 (kg), M2 = 2500 (kg), M3 = 3000 (kg). 
 Độ cao rơi của đầu búa là : H = 180 (cm). 
 Đệm đầu cọc dạng không thứ nguyên:  = CL/EF = 0.138 
TVC= 0.02509 s , M = 2100 (kg) 
 Kết quả tính ứng suất tại x= 0.00 cm 
Thời gian ứng suất 
0.0000 0.000 
0.0030 504.612 
0.0060 897.474 
0.0090 1124.441 
0.0120 1214.255 
0.0150 1180.670 
0.0180 1004.107 
0.0210 656.354 
0.0240 179.439 
0.0260 0.000 
Giá trị LN của US là :1216.785 N/cm2 
Tại thời điểm t=0.01264 s 
 Hình 1: Đồ thị ứng suất tại đầu cọc 
 6 
Kết quả tính ứng suất tại x=1400.00 cm 
TVC= 0.02509 s , M = 2100 (kg) 
Thời gian ứng suất 
0.0000 0.000 
0.0030 0.000 
 0.0060 465.939 
 0.0090 1114.461 
 0.0120 1618.594 
 0.0150 1240.909 
 0.0180 567.465 
 0.0210 200.146 
 0.0240 63.413 
 0.0260 -11.203 
Giá trị LN của US là : 1641.185 N/cm2 
Tại thời điểm t=0.011790 s 
 Hình2: Đồ thị ứng suất tại đáy cọc 
v. kết luận 
 Để nâng cao hiệu quả khi đóng cọc, nếu tăng khối lượng đầu búa lên ứng suất nén cực đại 
tại đáy cọc tăng và thời gian va chạm sẽ tăng. 
Kết quả tính ứng suất tại x=0.00 cm 
TVC= 0.02733 s , M = 2500 (kg) 
Thời gian ứng suất 
0.0000 0.000 
 0.0030 506.742 
 0.0060 913.097 
 0.0090 1171.265 
 0.0120 1310.156 
 0.0150 1339.758 
 0.0180 1233.697 
 0.0210 952.616 
 0.0240 522.632 
 0.0280 0.000 
Giá trị LN của US là : 1342.542 N/cm2 
Tại thời điểm t=0.01434 s 
Kết quả tính ứng suất tại x=0.00 cm 
TVC= 0.02971 s , M = 3000 (kg) 
Thời gian ứng suất 
0.0000 0.000 
 0.0030 508.610 
 0.0060 926.898 
 0.0090 1213.144 
 0.0120 1397.481 
 0.0150 1488.096 
 0.0180 1454.314 
 0.0210 1248.466 
 0.0240 883.461 
0.0300 0.000 
Giá trị LN của US là : 1495.790N/cm2 
Tại thời điểm t=0.01598 s 
Kết quả tính ứng suất tại x=1400.00 cm 
TVC= 0.02733 s , M = 2500 (kg) 
Thời gian ứng suất 
0.0000 0.000 
0.0030 0.000 
 0.0060 467.375 
 0.0090 1133.927 
 0.0120 1688.961 
 0.0150 1393.674 
 0.0180 809.740 
 0.0210 516.052 
 0.0240 429.783 
0.0280 48.948 
Giá trị LN của US là : 1706.696 N/cm2 
Tại thời điểm t=0.011791s 
Kết quả tính ứng suất tại x=1400.00 cm 
TVC= 0.02971 s , M = 3000 (kg) 
Thời gian ứng suất 
0.0000 0.000 
0.0030 0.000 
 0.0060 468.633 
 0.0090 1151.076 
 0.0120 1751.621 
 0.0150 1532.068 
 0.0180 1035.266 
 0.0210 822.118 
 0.0240 804.341 
 0.0270 713.530 
Giá trị LN của US là : 1764.975 N/cm2 
Tại thời điểm t=0.011792 s 
 7 
 Trong ba loại búa nêu trên khi ta chọn loại đầu búa có khối lượng 2500 (Kg) để đóng cọc, 
cọc đóng được an toàn và hiệu quả cao. Còn khi chọn đầu búa có khối lượng 3000 (kg ) cọc có 
khả năng vỡ. 
( Công trình này được sự tài trợ của Trung tâm KHTN Quốc gia v à Bộ tài nguyên môi trường) 
Tài liệu tham khảo. 
 [1]. Nguyễn Thúc An - ĐHTL – năm 1975: Lý thuyết va chạm và ứng dụng vào thi công 
móng cọc. 
 [2]. Nguyễn Thúc An - ĐHTL – năm 1979: áp dụng lý thuyết sóng vào bài toán đóng cọc 
 [3] Nguyễn Trọng Tư – năm 1999 : áp dụng lý thuyết va chạm dọc của thanh đàn hồi vào bài 
toán đóng cọc.( Luận án Thạc Sỹ kỹ thuật) 
 [4]. Khổng Doãn Điền – Bùi Quang Nhung – Phạm Đình Văn năm 2003: Nghiên cứu ảnh 
hưởng của Khối lượng - Đệm đầu cọc-Diện tích tiết diện ngang của cọc – Chiều cao rơi đến 
lực nén của đệm lên đầu cọc.( Tạp chí khoa học kỹ thuật Thuỷ lợi & môi trường số 1 tháng 6 
năm 2003. 
 [5]. Cung Nhất Minh, Diệp Vạn Linh, Lưu Hưng Lục năm 1999 ( Thí nghiệm và kiểm tra chất 
lượng cọc NXBXD Hà nội). 
Abstract 
Influence of volume-hammer to max stress of the concrete pile which was driven into 
identical foundation with the bottom of the pile put on the hard foundation. 
There is a comment in the article: If volume- hammer increases, the max compressive stress 
at the bottom of the pile and shock- time will increase. 
Authors used three hammers in this article and chose volume- hammer as 2,5 tons as among 
them, that is the best result.