Bài giảng Cơ học lý thuyết - Tuần 6 - Nguyễn Duy Khương
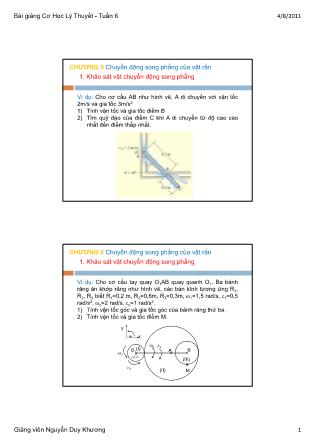
Ví dụ: Cho cơ cấu AB như hình vẽ, A di chuyển với vận tốc
2m/s và gia tốc 3m/s2
1) Tính vận tốc và gia tốc điểm B
2) Tìm quỹ đạo của điểm C khi A di chuyển từ độ cao cao
nhất đến điểm thấp nhất.
Bạn đang xem tài liệu "Bài giảng Cơ học lý thuyết - Tuần 6 - Nguyễn Duy Khương", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cơ học lý thuyết - Tuần 6 - Nguyễn Duy Khương
Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 1 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Ví dụ: Cho cơ cấu AB như hình vẽ, A di chuyển với vận tốc 2m/s và gia tốc 3m/s2 1) Tính vận tốc và gia tốc điểm B 2) Tìm quỹ đạo của điểm C khi A di chuyển từ độ cao cao nhất đến điểm thấp nhất. CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Ví dụ: Cho cơ cấu tay quay O1AB quay quanh O1. Ba bánh răng ăn khớp răng như hình vẽ, các bán kính tương ứng R1, R2, R3 biết R1=0,2 m, R2=0,6m, R3=0,3m, 1=1,5 rad/s, 1=0,5 rad/s2, c=2 rad/s, c=1 rad/s2. 1) Tính vận tốc góc và gia tốc góc của bánh răng thứ ba. 2) Tính vận tốc và gia tốc điểm M. O1 A B1 (I) (II) (III) + x y c 1 c M Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 2 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B1 (I) (II) (III) + x y c 1 c M 1) Tính vận tốc góc và gia tốc góc của bánh răng thứ ba Theo công thức villit ta có: 1 1 ( 1)ic n n c R R 11 3 13 ( 1)c c R R 1 3 3 1c c R R 3 0, 22 1,5 20,3 3 13 ( / ) 3 rad s CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B1 (I) (II) (III) + x y c 1 c M Theo công thức villit ta có: 1 1 ( 1)ic n n c R R 1 3 3 1c c R R 3 0, 2( 1) 0,5 ( 1)0,3 2 3 2( / )rad s Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 3 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B1 (I) (II) (III) + x y c 1 c M *Bài toán vận tốc /M B M BV V V 2) Tính vận tốc và gia tốc điểm M Ta chọn B làm cực ta có công thức quan hệ sau33 BV /M BV Do B quay quanh O1 nên 1 1 2 3. ( 2 )B c cV O B j R R R j Do M có chuyển động quay quanh B nên / 3 3M BV R i 1 2 3 3 3( 2 )M cV R R R j R i 130,3 (0, 2 2.0,6 0,3)2 3 i j 1,3 2,2i j CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B1 (I) (II) (III) x y c 1 c M Cách 2: Ta có thể tính vận tốc bằng công thức vector 33 1 2 3 3 30; 2 ;0 ;0;0M cV R R R R 1,3 2,2i j /M B M BV V V 3M BV V BM 1 3c O B BM Với 1 1 2 3 1 2 32 2 ;0;0O B R R R i R R R 30; ;0BM R 0;0;c c 3 30;0; 3 3 1 2 3; 2 ;0cR R R R BM 1 O B Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 4 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B 1 (I) (II) (III) + x y c 1 c M *Bài toán gia tốc /M B M BW W W 2) Tính vận tốc và gia tốc điểm M 33 BW /M B W Do B quay quanh O1 nên n B B BW W W Do M có chuyển động tương đối quay quanh B nên 2 21 2 3 3 3 3 3 1 2 32 2M c cW R R R R i R R R R j 5 4,5i j 2 1 1c cO B i O B j nBW / / / n M B M B M BW W W / n M BW 2 3 3 3 3R i R j 22 130,2 2.0,6 0,3 2 0,3.2 0,3 0,2 2.0,6 0,3 13i j CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng O1 A B 1 (I) (II) (III) c 1 c M /M B M BW W W 33 Cách 2: Ta có thể tính vận tốc bằng công thức vector 2 3 3BW BM BM 2 1 1 2 3 3 c cO B O B BM BM Với 0;0;c c 1 1 2 32 ;0;0O B R R R 3 30,0, 30; ;0BM R 2 1 2 3 1 2 3 2 3 3 3 3 0; 2 ;0 2 ;0;0 ;0;0 0; ;0 M c cW R R R R R R R R 2 21 2 3 3 3 3 3 1 2 3;2 2 0;c cR R R R R R R R x y BM 1O B Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 5 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Ví dụ: Cho mô hình như hình vẽ. Biết AB=BC=R Tính vận tốc góc và gia tốc góc của thanh BC, CD. 45o A B C D R R R 11 22 *Phân tích chuyển động Giải + Điểm B quay tròn quanh A + Điểm C quay tròn quanh D CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng *Giải bài toán vận tốc A B C D1 2 CV BV +Tính vận tốc VB BV R +Tính vận tốc VC (Có 3 cách tính VC) Cách 1: Dùng công thức quan hệ vận tốc /C BV 1 2 2 0 2 R R |_ CD |_ AB |_ BC 12R R 2R Chiếu (*) lên trục x, y Ox: /C B C BV V V (*) 1 Oy: 1 20R R 2 Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 6 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng 2 A B C D1 CV BV Cách 2: Dùng tâm vận tốc tức thời P 12 2R R 1 2 CB VV PB PC (**) 2 C B PC RV V R PB R (**) 2 BV R PB R (**) CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng A B C D 1 2 AB /C B C BV V V (*) Cách 3: Dùng phép tính vector DC BC 1 2DC AB BC 0,0, 1 10,0, 2 20,0, 0, ,0AB R ,0,0BC R , ,0DC R R 1 1 2, ,0 ,0,0 0, ,0R R R R 1 1 2, ,0 , ,0R R R R 1 1 2 R R R R 1 2 Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 7 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng *Giải bài toán gia tốc +Tính gia tốc tại C (Chọn B làm cực) /C B C BW W W Chiếu (***) lên trục x, y A B C D 1 2 2 1 (***)/ / n n n C C B B C B C BW W W W W W |_ CD // CD 12R 212R |_ AB // AB R 2R |_ BC // BC 2R 22R 1 2 2 1 2 2 22 2 2 2 R R R R 1 2 2 2 1 2 22 2 2 2 R R R R BW /C BW / n C BW CW n CW n BW 1 2 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng A B C D Cách 2: Dùng phép tính vector 0,0, 1 10,0, 2 20,0, 0, ,0AB R ,0,0BC R , ,0DC R R 1 2 2 1 / / n n n C C B B C B C BW W W W W W 2 2 1 1 2 2 2 DC DC AB AB BC BC 2 2 11 1 2 2 2 , ,0 , ,0 ,0,0 0, ,0 0, ,0 ,0,0 R R R R R R R R AB DC BC Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 8 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Ví dụ: Cho mô hình như hình vẽ. Biết R=3r=0,6m, tâm B chuyển động theo phương ngang với vận tốc VB=2m/s và gia tốc WB=1m/s2. Con lăn B lăn không trượt, bỏ qua ma sát ròng rọc C, dây không co giãn, bỏ qua khối lượng dây và ròng rọc C. Tính vận tốc và gia tốc của tải A *Phân tích chuyển động Giải + Con lăn B chuyển động song phẳng + Tải A chuyển động tịnh tiến A + x y B C BV BW I H CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Vì I là tâm vận tốc tức thời nên A + x y B C BV I H B . 2H B B BV IH R r r 2A H BV V V 2 2BH B VV r V r Do dây không co giãn nên VA có phương thẳng đứng và hướng như hình vẽ HV AV Con lăn B lăn không trượt nên tâm vận tốc tức thời tại I nên B B B V V BI r *Bài toán vận tốc 2.2 4( / )m s Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 9 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng A + x y B C BW I H B AV Theo công thức quan hệ gia tốc ta có: /H B H BW W W *Bài toán gia tốc / / n B H B H BW W W (Chọn B làm cực) / / n B H B H BW i W j W i / /nB H B H BW W i W j 2. .B B BW HB i HB j 2 2 3 BB VW i j r Do tâm B chuyển động tịnh tiến nên BB B B d rdVW r dt dt BB Wr CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng A + x y B C BW I H B AW Do dây không co giãn nên 2A Hx BW W W 22( / )m s WA có phương thẳng đứng và hướng như hình vẽ Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011 Giảng viên Nguyễn Duy Khương 10 CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Bài tập về nhà Cho cơ cấu như hình vẽ, tìm vận tốc và gia tốc của điểm M, N, H O1 A B1 (I) (II) (III) 1 M c c N H O1 A B1 (I) (II) (III) c 1 c M M N H CHƯƠNG 9 Chuyển động song phẳng của vật rắn 1. Khảo sát vật chuyển động song phẳng Bài tập về nhà Cho cơ cấu như hình vẽ, tìm vận tốc góc và gia tốc góc của thanh O2B và AB O1 1 1 O2 A B 1 2 1 2 2 2 3 2 O A O B a OO a O1 1 1 O2 A B 1 2 1 2 2 2 2 O A O B a OO a O1 1 1 O2 A B 1 2 1 2 2 O A O B a OO a O1 1 1 O2 A B 1 2 1 2 3 1 2 O A O B a OO a
File đính kèm:
 bai_giang_co_hoc_ly_thuyet_tuan_6_nguyen_duy_khuong.pdf
bai_giang_co_hoc_ly_thuyet_tuan_6_nguyen_duy_khuong.pdf

