Bài giảng Trình biên dịch - Chương 3: Phân tích từ vựng

CHƯƠNG 3
PHÂN TÍCH TỪ VỰNG 
3.1. Vai trò cuả bộ phân tích từ vựng
1. Token, mẫu, trị từ vựng
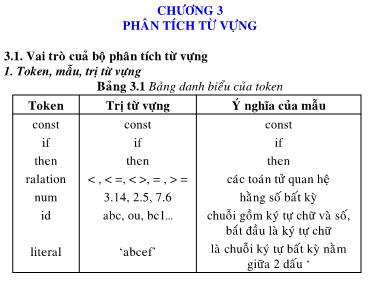
Bảng 3.1 Bảng danh biểu của token
Token Trị từ vựng Ý nghĩa của mẫu
const
if
then
ralation
num
id
literal
const
if
then
, = , > =
3.14, 2.5, 7.6
abc, ou, bc1
‘abcef’
const
if
then
các toán tử quan hệ
hằng số bất kỳ
chuỗi gồm ký tự chữ và số, 
bắt đầu là ký tự chữ
là chuỗi ký tự bất kỳ nằm
giữa 2 dấu ‘
Hình 3.1. Sự giao tiếp giữa bộ phân tích từ vựng và bộ phân tích
cú pháp
3.2. CÁC TÍNH CHẤT CỦA TOKEN
3.3. CHỨA TẠM CHƯƠNG TRÌNH NGUỒN
1. Cặp bộ đệm
Cấu tạo
Bộ phân tích
từ vựng
Bảng danh biểu
Bộ phân
tích CP
Chương trình
nguồn token
yêu cầu token
A : = B * . - 2 eof
p1 p2
Hình 3.2. Cặp bộ đệm
Quy trình hoạt động
Giải thuật:
if p2 ở ranh giới một nửa bộ đệm then
begin lấp đầy N ký hiệu nhập mới vào nửa bên phải
p2 := p2 + 1;
end 
else if p2 ở tận cùng bên phải bộ đệm then 
begin lấp đầy N kỳ hiệu nhập vào nửa bên trái bộ đệm
chuyển
p2 về ký tự tận cùng bên trái của bộ đệm end
else p2 := p2 + 1;
2. Phương pháp cầm canh
A : = B * X EOF - 2 EOF EOF
N ký tự N ký tự
p1 p2
Hình 3.3. Cặp bộ đệm theo phương pháp cầm canh
Giải thuật:
p2 := p2 + 1;
if p2 ^ eof then 
if p2 ở ranh giới một nửa bộ đệm then 
begin
chất đầy N kỳ hiệu nhập vào nửa bên phải bộ đệm; 
p2 := p2 + 1 
end
else if p2 ở tận cùng bên phải bộ đệm then 
begin
lấp đầy N ký hiệu vào nử bên trái bộ đệm; chuyển p2 
về đầu bộ đệm
end
else /* dừng sự phân tích từ vựng */
3.4. Đặc tả token
Các quy tắc định nghiã biểu thức chính quy
1. ∈ là biểu thức chính quy, biểu thị cho tập {∈}
2. a là ký hiệu thuộc Σ, biểu thị cho tập {a}
3. r và s là hai biểu thức chính quy, biểu thị cho L (r) và L (s) thì:
ø a) (r) | (s) là biểu thức chính quy, biểu thị cho L(r) ∪ L(s).
b) (r) (s) là biểu thức chính quy, biểu thị cho L(r) L(s).
c) (r)* là biểu thức chính quy, biểu thị cho (L(r))*.
d) r là biểu thức chính quy, biểu thị cho L(r).
Thí dụ 3.1. Cho Σ = {a, b}
1. a|b 
2. (a| b) | (b| a) 
3. a*
Hai biểu thức chính quy tương đương r và s, ký hiệu r = s.
2. Định nghĩa chính quy
Nếu Σ là tập ký hiệu căn bản, thì định nghiã chính quy là chuỗi định
nghiã có dạng: d1→ r1
dn→ rn
Thí dụ 3.2. letter → A | B | |Z | a| b || z
digit → 0 |1| | 9
id→ letter ( letter | digit)*
Thí dụ 3.3. digit→ 0 | 1 | | 9 
digits → digit digit*
optional_fraction → .digits | ∈
optional_exponent → (E (+| - |∈) digits) | ∈
3.5. Nhận dạng token
Thí dụ 3.4. Cho văn phạm G:
stmt→ if exp then stmt 
| if exp then stmt else stmt 
| ∈
exp → term relop term | term
term → id | num
Định nghĩa chính quy
if → if then → then else→ else 
relop → | >= | | = 
id → letter (letter | digit)* 
num → digit+ (.digit+ | ∈) ( E ( + | - | ∈) digit+ | ∈ )
delim→ blank | tab | newline
ws → delim+
Từ định nghĩa chính quy ta xây dựng bảng mẫu cho token như ở bảng
3.3 trang 74.
3.6. Sơ đồ dịch
1. Miêu tả
0 7
8
Bắt đầu >
=
other
2
3
Start < = return (relop, LE)
6 7
8
> return (relop, NE)
4 return (relop, LT)
5
=
return (relop, EQ)
>
other
6 Hình 3.4. Sơ đồ dịch cho >= 
và =
0 1
=
other
(relop, EQ)
return (relop, EQ)
*
*
*
Hình 3.5. Sơ đồ dịch nhận dạng token relop
Lưu ý: 
- Phần khai báo bao gồm khai báo hằng, biến biểu thị và các định
nghĩa chính quy.
- Phần quy tắc biên dịch là các phát biểu có dạng:
p1→ {hành vi ngữ nghĩa 1}
p2→ {hành vi ngữ nghĩa 2}
pn → {hành vi ngữ nghĩa n}
3.8. Automat hữu hạn
1. Automat hữu hạn không tất định (NFA)
Thí dụ: Cho NFA: 
Tập trạng thái S = {0, 1,2, 3}; Σ = {a, b}; Trạng thái bắt đầu so = 0; 
Tập trạng thái kết thúc F = {3}. 
Bảng 3.4. Bảng truyền cho NFA ở hình 3.10
Ký hiệu nhập
Trạng thái
a b
0 {0, 1} {0}
1 - {2}
2 - {3}
NFA chấp nhận một chuỗi nhập x nếu và chỉ nếu tồn tại một đường
nào đó trong sơ đồ từ trạng thái bắt đầu đến trạng thái kết thúc sao
cho tất cả tên của các cạnh con đường cho chuỗi x. NFA chấp nhận
chuỗi aabb.
2. Automat hữu hạn tất định (DFA)
DFA là trường hợp đặc biệt của NFA, nó không có:
i) Sự truyền rỗng.
ii) Với mỗi trạng thái s và ký hiệu nhập a chỉ tồn tại nhiều nhất một
cạnh có tên a xuất phát tư øs.
Giải thuật 3.1.Mô phỏng hoạt động của DFA trên chuỗi nhập x.
Thí dụ 3.5
start
30 a 0
a b b1 1
Hình 3.12. DFA nhận dạng ngôn ngữ (a | b)*abb
3. Chuyển NFA sang DFA
Giải thuật 3.2. Xây dựng tập con (Tạo DFA từ NFA).
Nhập: Cho NFA gọi là N.
Xuất: DFA gọi là D, nhận dạng cùng ngôn ngữ như NFA.
Phương pháp: Xây dựng bảng truyền cho D. Mỗi trạng thái của D là
tập trạng thái của N. D mô phỏng đồng thời mọi chuyển động của N 
trên chuỗi nhập cho trước bằng các tác vụ:
∈-closure (s); ∈-closure (T); move (T, a)
Mô phỏng 3.2. Xây dựng tập con
Giải thuật: Tính ∈-closure
Đẩy tất cả các trạng thái trong T lên stack; Khởi tạo ∈-closure (T) 
cho T.
Mô phỏng 3.3. Tính ∈-closure
Thí dụ 3.6. (H.3.13 ) là NFA nhận dạng ngôn ngữ (a | b )* abb. Chúng
ta dùng giải thuật 3.2 để xây dựng DFA tương đương.
0start
∈
1 10
4∈
a
b
b
a
2
8
3
5
6 7 9
∈
∈
∈
Hình 3.13. NFA nhận dạng (a | b)* abb
b
3.9. Từ biểu thức chính quy đến NFA
Xây dựng NFA từ biểu thức chính quy
Giải thuật 3.3. Xây dựng NFA từ biểu thức chính quy (Cấu trúc
Thompson’)
Nhập: Biểu thức chính quy r trên Σ.
Xuất: NFA nhận dạng ngôn ngữ L (r).
Phương pháp:
Quy tắc:
1. Với ∈ , xây dựng NFA
2. Với a thuộc Σ, xây dựng NFA
start
i f
∈
start
i f
a
3. Giả sử N( s ) vàN( t ) là NFA cho biểu thức chính quy s và t
- Với s | t xây dựng NFA hỗn hợp N (s| t)
i
start f
∈N(s)
N(t) ∈∈
∈
- Với biểu thức st, xây dựng NFA hỗn hợp N (st)
start
i f
N(t)N(s)
- Với biểu thức s* , xây dựng NFA N (s*)
start
i f
∈
∈
∈
∈
- Biểu thức s thì N (s) là NFA nhận dạng L (s)
Các tính chất cuả NFA xây dựng theo cấu trúc Thompson’
Thí dụ 3.7.
Giải thuật 3.4. Mô phỏng NFA
Nhập: NFA gọi là N được xây dựng theo giải thuật 3.3, chuỗi nhập x. 
X được kết thúc bằng eof, N có trạng thai bắt đầu s0 và tập trạng thái
kết thúc F.
Xuất: Giải thuật trả lời đúng nếu N chấp nhận x, ngược lại trả lời sai
Phương pháp:
Giải thuật: Mô phỏng 3.4.
Thí dụ 3.8. Giả sử ta có NFA ở (H.3.13 ), x là chuỗi nhập chứa a. 
Dùng giải thuật 3.4 xét xem NFA có chấp nhận x ?. Kết qủa giải thuật
trả lời sai ( nghiã là a không thuộc ngôn ngữ do NFA nhận dạng
Thời gian và không gian cần thiết cho việc nhận dạng một chuỗi nhập:
- Đối với DFA: không gian O (2 ( )) và thời gian O (|x | ).
- Đối với NFA: không gian O (|r | ) và thời gian O (| r | * | x | ).
3.10. Xây dựng DFA trực tiếp từ biểu thức chính quy và vấn đề tối
ưu hóa việc so trùng mẫu
1. Trạng thái quan trọng của NFA
Trạng thái quan trọng là từ nó có sự truyền khác rỗng. Như vậy nếu
hai tập trạng thái có cùng số trạng thái quan trọng thì chúng được
đồng nhất. NFA được xây dựng theo cấu trúc Thompson’ có trạng thái
kết thúc không có sự truyền ra, như vậy nó không phải là trạng thái
quan trọng ( nhưng thực sự nó lại rất quan trọng ). Để tránh tình trạng
này người ta thêm ký hiệu # vào sau biểu thức chính quy, và trạng
thái kết thúc có sự truyền trên ký hiệu #. Khi xây dựng tập con hoàn
tất thì trạng thái nào có sự truyền trên # là trạng thái chấp nhận.
- Biểu thức r# được gọi là biểu thức chính quy gia tố.
Văn phạm của biểu thức chính quy:
exp → exp | term exp → term term → term • factor
term → factor factor → factor* factor → ( exp )
factor → a factor → b
Hình 3.16. Cây phân rã của biểu thức gia tố (a| b )* abb#
a
3
b
4
#
6b
5
a
1
b
2
*
• •
• •
Hình 3.17. NFA được xây dựng từ ( a| b )* abb#
Lưu ý:
- Các trạng thái được ký hiệu bằng số là trạng thái quan trọng; Các
trạng thái được ký hiệu bằng chữ là trạng thái không quan trọng.
- Ở thí dụ 3.6 trạng thái A và C có cùng số trạng thái quan trọng là
2,4,7 , trong (H 3.17) là 1,2,3:
A = {0,1,2,4,7} C = {1,2,4,5,7}
Astart
∈
B F
2∈
a
#
b
a
1
4
C
D
F 3 6
∈
∈
∈ b4 ba
∈
∈
∈
Bảng 3.6. Các quy tắc để tính ba hàm nullable, firstpos, lastpos
Nút n nullable (n) firstpos (n) lastpos (n)
n là nút có tên
là ∈
true
n là nút có tên
là vị trí i false {i} {i}
nullable(c1) or
nullable(c2)
firstpos(c1) ∪
firstpos(c2)
lastpos(c1) ∪
lastpos(c2)
nullable(c1) and
nullable(c2)
if nullable(c1) 
then firstpos(c1) ∪
firstpos(c2) 
else firstpos(c1)
if nullable(c2) 
then lastpos(c1) ∪ lastpos(c2) 
else lastpos(c2)
true firstpos(c1) lastpos(c1)
n
c2c1
|
c2c1
° n
c1
∗ n
Các quy tắc tính hàm followpos (n):
1. Nếu nút n là nút cat với con bên trái là c1, con bên phải là c2 và i là
vị trí trong lastpos(c1), thì tất cả vị trí trong first(c2) sẽ cho vào
followpos(i).
2. Nếu n là nút star và i là vị trí trong lastpos(n) thì tất cả các vị trí
trong firstpos(n) sẽ cho vào followpos(i).
Thí dụ 3.10. Ta xác định DFA cho biểäu thức (a | b)* abb
{1}a {1} {2}a {2}
# {6}
∗
{1,2} {1,2}
{1,2} {1,2}
{5}a{5}
{4}a{4}
{3}a{3}
{1,2,3}
{1,2,3} {1,2,3}
{1,2,3}
{3}
{4} {5}
{6}
{6}
Hình 3.19. Tính các hàm nullable, firstpos, lastpos cho các nút trên cây
phân tích của biểu thức ( a| b )* abb
Sau đó ta tính hàm followpos.
Bảng 3.7. các trị followpos của các nút trên cây ở (H.3.19) 
Nút followpos
1 {1,2,3}
2 {1,2,3}
3 {4}
4 {5} 
5 {6} 
6 _
Giải thuật 3.5. Xây dựng DFA từ biểu thức chính quy
Nhập: Biểu thức chính quy r.
Xuất: DFA gọi là D, nhận dạng ngôn ngữ L( r)
Phương pháp :1. Xây dựng cây phân tích cho BTCQ gia tố r#.
2. Tính các hàm nullable, firstpos, lastpos và followpos cho các nút
trên cây phân tích
3. Xây dựng các trạng thái, hàm truyền và bảng truyền cho D bằng
thủ tục ở (mô phỏng 3.5).
Thủ tục tạo tập con là các trạng thái của DFA:
Lúc đầu D chỉ có một trạng thái bắt đầu là firstpos(root) , chưa được
đánh dấu.
Mô phỏng 3.5. Thủ tục tạo tập con
while có trạng thái T chưa được đánh dấu, trong tập trạng thái
của D do begin đánh dấu T;
for với mỗi ký hiệu nhập a do;
begin với U là tập các vị trí trong followpos (p), p là vị trí trong
T, sao cho ký hiệu tại vị trí p là a;
if U không rỗng và chưa có trong tập trạng thái của D
then begin thêm U vào tập trạng thái của D và là trạng thái
chưa được đánh dấu;
D[T, a] := U;
end;
end;
end;
Lưu ý: trạng thái kết thúc của D có chứa vị trí của y.
Thí dụ 3.10. Xây dựng DFA từ btcq ( a| b )* abb. (trang 103 -104)
3. Tối thiểu số trạng thái của DFA
- Khái niệm DFA đầy đủ, trạng tái chết d.
- Chuỗi w phân biệt trạng thái s với trạng thái t.
Thí dụ: DFA ở (H.3.14, tr. 90), nếu xuất phát từ C để nhận dạng w=bb 
thì không đi được đến trạng thái chấp nhận, ngược lại từ B thì đi đến E 
là trạng thái chấp nhận.
Giải thuật 3.6. Tối thiểu số trạng thái của DFA.
Nhập: DFA, gọi là M có S, Σ, s0, F. M là DFA đầy đủ.
Xuất: DFA, gọi là M’ chấp nhận ngôn ngữ như M, với số trạng thái
nhỏ nhất.
Phương pháp: 
1.Tạo Π khởi đầu có 2 nhóm: các trạng thái kết thúc F, và các trạng
thái không kết thúc S – F.
2. Áp dụng thủ tục (mô phỏng 3.6) để tạo Πnew .
3. Nếu Πnew = Π thì Πfinal = Π, tiếp tục bước 4, ngược lại lặp lại bước
2, với Π = Πnew
4. Chúng ta chọn mỗi nhóm 1 trạng thái đại diện và đó là trạng thái
của M’ .
5. Nếu M’ có trạng thái chết d thì loại nó ra khỏi M’. Tất cả các sự
truyền đến trạng thái d đều không xác định.
Mô phỏng 3.6. Giải thuật tạo Πnew
for với mỗi nhóm G của Π do begin
- chia G thành các nhóm nhỏ hơn sao cho hai trạng thái s và t 
của G sẽ ở cùng một nhóm nhỏ hơn nếu và chỉ nếu các sự truyền trên
tất cả các ký hiệu nhập a từ s và t đều đi đến các trạng thái kế tiếp ở
trong cùng một nhóm của Π;
- ta thay G bằng các nhóm nhỏ hơn vừa được tạo nên, cho
chúng vào Πnew ;
end; 
Thí dụ 3.11. Cho DFA như ở (H. 3.14, tr. 90).
Cách giải ở tr. 106 – 107.
4. Các phương pháp nén bảng truyền FA
1. Thu giảm hàng và cột dư thừa
Hình 3.21. Bảng truyền được nén bằng phương pháp thu giảm hàng và
cột dư thừa
0 – 0 1 0000 222222222 0 – 0 3 0 – 0 
0
1
2
3
4
4
0 0 -1 3 1 -1
1 1 -1 2 1 5
2 2 -1 -1 2 5
3 3 -1 -1 2 -1
4 4 -1 -1 -2 -1
5 4 -1 -1 4 -1
0 1 2 3
yrmap
y next
2. Nén cặp
Hình 3.22. Bảng truyền nén theo phương pháp nén cặp
0 • 7 ‘0’,3 ‘0’,1 ‘1’,1 ‘2’,1 ‘3’,1 ‘4’,2 ‘5’,2 ynext 0
1 • 0 -1-112-1..1111111111-1-1 5-1 ynext 1
2 • 6 ‘0’,2 ‘1’,2 ‘2’,3 ‘3’,4 ‘4’,1 ‘5’,1 ynext 2
3 • 7 ‘0’,1 ‘1’,1 ‘2’,2 ‘3’,2 ‘4’,2 ‘5’,2 ‘6’,2 ynext 3
4 • 7 ‘0’,4 ‘1’,4 ‘2’,4 ‘3’,2 ‘4’,2 ‘5’,2 ‘6’,2 ynext 4
5 • 6 ‘0’,2 ‘1’,2 ‘2’,2 ‘3’,2 ‘4’,1 ‘5’,1 ynext 5
ynext
Mô phỏng 3.7. Giải thuật tìm trạng thái kế tiếp trên bảng truyền đã
được nén
row := ynext [t];
I := row^[0], /* row^ là ma trận 1 chiều ynext t */
if I = 0 then
begin c := ord (a)
s := row^[c]; /* s là trạng thái kế tiếp */
end
else begin
while (a row^ [i]. chart) and (i < I) do
i := i + 1;
if a = row^[i]. chart then s := row^[i]. State
else writen (‘sai – lỗi từ vựng’);
end;
3.11. Thiết kế bộ sinh bộ phân tích từ vựng
Hình 3.23. Trình biên dịch Lex và Bộ phân tích từ vựng
Chương trình mô phỏng FA và
bảng truyềnTrình biên dịch
Lex
a)
Chương trình
mô phỏng FA
Bảng truyền
b)
Đặc tả lex
Bộ đệm nhập
1. Mẫu so trùng trên cơ sở NFA
Hình 3.24. NFA được tao ra từ sự đặc tả LEX
so N(pi)
∈
∈
N(p1)
N(pn)
∈