Bài giảng Cơ học kết cấu 1 - Chương 2: Phân tích cấu tạo hình học của các hệ phẳng
§ 2.1 KHÁI NIỆM
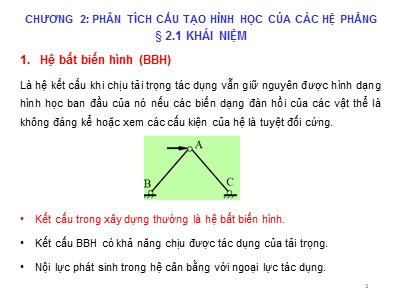
Hệ bất biến hình (BBH)
Là hệ kết cấu khi chịu tải trọng tác dụng vẫn giữ nguyên được hình dạng hình học ban đầu của nó nếu các biến dạng đàn hồi của các vật thể là không đáng kể hoặc xem các cấu kiện của hệ là tuyệt đối cứng.
Kết cấu trong xây dựng thường là hệ bất biến hình.
Kết cấu BBH có khả năng chịu được tác dụng của tải trọng.
Nội lực phát sinh trong hệ cân bằng với ngoại lực tác dụng.
Bạn đang xem tài liệu "Bài giảng Cơ học kết cấu 1 - Chương 2: Phân tích cấu tạo hình học của các hệ phẳng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Cơ học kết cấu 1 - Chương 2: Phân tích cấu tạo hình học của các hệ phẳng
CHƯƠNG 2: PHÂN TÍCH CẤU TẠO HÌNH HỌC CỦA CÁC HỆ PHẲNG § 2.1 KHÁI NIỆM Hệ bất biến hình (BBH) Là hệ kết cấu khi chịu tải trọng tác dụng vẫn giữ nguyên được hình dạng hình học ban đầu của nó nếu các biến dạng đàn hồi của các vật thể là không đáng kể hoặc xem các cấu kiện của hệ là tuyệt đối cứng. Kết cấu trong xây dựng th ư ờng là hệ bất biến hình. Kết cấu BBH có khả năng chịu được tác dụng của tải trọng. Nội lực phát sinh trong hệ cân bằng với ngoại lực tác dụng. 1 2. Hệ biến hình (BH) Là hệ kết cấu khi chịu tải trọng tác dụng sẽ thay đổi hình dạng hình học ban đầu một cách hữu hạn mặc dù coi các biến dạng đàn hồi của các vật thể là không đáng kể hoặc xem các cấu kiện của hệ là tuyệt đối cứng . Kết cấu biến hình không có khả năng chịu tải trọng Công trình xây dựng không dùng hệ BH 2 3. Hệ biến hình tức thời (BHTT) Là hệ kết cấu khi chịu tải trọng tác dụng sẽ thay đổi hình dạng hình học ban đầu của nó vô cùng bé (Nếu bỏ qua các đại lượng vô cùng bé bậc cao về sự thay đổi kích thước hình học) mặc dù xem các cấu kiện của hệ là tuyệt đối cứng. Sau khi thay đổi hình dạng hình học vô cùng bé hệ lại trở nên BBH Nội lực phát sinh trong hệ thường rất lớn Kết cấu trong xây dựng không dùng hệ BHTT 3 4. Miếng cứng Là một hệ phẳng bất kỳ bất biến hình một cách rõ rệt . Quy ước biểu diễn miếng cứng 5. Bậc tự do Là số thông số độc lập đủ để xác định vị trí của hệ đối với một hệ khác được xem là bất động. Một điểm trong mặt phẳng có hai bậc tự do là hai chuyển động theo hai phương bất kỳ khác nhau 4 5 Một miếng cứng có ba bậc tự do là hai chuyển động theo hai phương bất kỳ khác nhau và một chuyển động quanh giao điểm của hai phương đó. § 2.2 CÁC LOẠI LIÊN KẾT Liên kết đơn giản Là liên kết chỉ nối hai miếng cứng lại với nhau 1.1. Liên kết thanh (liên kết loại 1) Cấu tạo: Gồm 1 thanh có khớp lý tưởng ở hai đầu Tính chất động học: Khử được 1 bậc tự do, ngăn không cho chuyển vị theo phương dọc trục. Tính chất tĩnh học: Xuất hiện một phản lực liên kết theo dọc trục thanh Gối di động là trường hợp đặc biệt của liên kết loại 1 6 1.2. Liên kết khớp (liên kết loại 2) Cấu tạo: gồm có 1 khớp lý tưởng tại điểm nối hai miếng cứng. Tính chất động học: khử được 2 bậc tự do, ngăn không cho chuyển vị theo 2 phương. Về mặt động học: liên kết khớp tương đương với hai liên kết thanh. Tính chất tĩnh học: Xuất hiện một phản lực liên kết tại khớp. Gối cố định là trường hợp đặc biệt của liên kết loại 2 7 1.3. Liên kết hàn (liên kết loại 3) Cấu tạo: gồm có 1 mối hàn tại điểm nối hai miếng cứng . Tính chất động học: khử được 3 bậc tự do, ngăn không cho chuyển vị theo 2 phương, c huyển vị xoay. Về mặt động học: liên kết khớp tương đương với ba liên kết thanh h ay 1 khớp cộng một thanh Tính chất tĩnh học: xuất hiện một phản lực liên kết tại khớp. Ngàm là trường hợp đặc biệt của liên kết loại 3 8 2. Liên kết phức tạp Là liên kết nối từ 3 miếng cứng với nhau trở lên , thường gặp liên kết khớp phức tạp hoặc hàn phức tạp Độ phức tạp của liên kết phức tạp: là số liên kết đơn giản cùng loại tương đương với liên kết phức tạp đó Công thức tính : p = D-1 (2.1) p : độ phức tạp của liên kết phức tạp D là số miếng cứng quy tụ vào liên kết phức tạp. 9 3. Các loại gối tựa Là liên kết nối công trình với đất 10 § 2.3 CÁCH NỐI CÁC MIẾNG CỨNG THÀNH HỆ BẤT BIẾN HÌNH Điều kiện cần: thể hiện mối liên hệ giữa số liên kết cần thiết với số lượng miếng cứng có trong hệ đang xét . 1.1. Hệ bất kỳ Hệ có D miếng cứng Điều kiện cần: T liên kết thanh n = T + 2K + 3H - 3(D-1) ≥0 (2.2) K liên kết khớp Có thể xảy ra ba trường hợp : H liên kết hàn. n hệ thiếu liên kết, kết luận : BH n=0 => hệ đủ liên kết có thể BBH n>0 => hệ thừa liên kết 11 1.2. Hệ nối đất Hệ có D miếng cứng Điều kiện cần: T liên kết thanh n = T + 2K + 3H+C - 3D ≥ 0 (2.3) K liên kết khớp Có thể xảy ra ba trường hợp: H liên kết hàn n hệ thiếu liên kết, kết luận : BH C liên kết tựa n=0 => hệ đủ liên kết có thể BBH tương đương loại 1 n>0 => hệ thừa liên kết 1.3. Hệ dàn Dàn là hệ gồm các thanh thẳng chỉ nối với nhau bằng các khớp ở hai đầu mỗi thanh . m ắt dàn 12 a. Dàn không nối đất Hệ có D thanh Điều kiện cần: M mắt n = D + 3 – 2M ≥ 0 (2.4) Có thể xảy ra ba trường hợp như trên b. Dàn nối đất Hệ có D thanh Điều kiện cần: M mắt n = D + C – 2M ≥ 0 (2.5) C liên kết tựa n hệ thiếu liên kết, kết luận : BH tương đương loại 1 n=0 => hệ đủ liên kết có thể BBH n>0 => hệ thừa liên kết 13 2. Điều kiện đủ: các liên kết cần được bố trí hợp lý 2.1. Cách nối một điểm (mắt) vào một miếng cứng thành hệ BBH Điều kiện cần và đủ để nối một điểm ( mắt) vào một miếng cứng thành một hệ BBH là phải dùng hai thanh không thẳng hàng. Hai thanh không thẳng hàng này g ọi là bộ đôi Bộ đôi không làm thay đổi tính chất động học của hệ 2.2. Cách nối hai miếng cứng thành một hệ BBH Dùng 3 liên kết tương đương loại 1 và được bố trí hợp lý: Dùng 3 liên kết thanh không đồng qui, không song song. Dùng 1 liên kết khớp và 1 liên kết thanh, phương của thanh không đi qua khớp. Sử dụng 1 liên kết hàn. 14 2.3. Cách nối ba miếng cứng thành một hệ BBH Dùng 6 liên kết tương đương loại 1 và được bố trí hợp lý: Sử dụng 6 liên kết thanh. Sử dụng 3 liên kết khớp. Sử dụng 2 liên kết hàn. Sử dụng 1 liên kết hàn, 1 liên kết khớp, 1 liên kết thanh. ... Điều kiện cần và đủ để nối 3 miếng cứng là ba khớp thực hoặc giả tạo tương hỗ ( giao điểm của hai thanh nối từng cặp hai miếng cứng) không được nằm trên cùng một đường thẳng. 15 2.4. Trường hợp tổng quát Sử dụng ba bài toán ở trên để nối các m iếng cứng lại với nhau để được các miếng cứng lớn hơn (số miếng cứng giảm đi). Sau đó dùng vẫn các bài toán trên để đưa về kết luận cuối cùng. 3. Ví dụ VD1: Khảo sát cấu tạo hình học của hệ kết cấu sau Điều kiện cần: hệ nối đất D = 3; T = 0; K = 2; H = 0; C = 5 Thay vào (2.3) hệ đủ liên kết có thể BBH 16 Điều kiện đủ: Ta thấy 2 miếng cứng AB (I) và CD (III) có hai khớp ở hai đầu nên coi như là liên kết thanh trục thanh đi qua hai khớp . Miếng cứng BCE liên kết với trái đất bằng 3 thanh AB, EF và DC. Nếu ba thanh này đồng quy hệ sẽ biến hình tức thời. Để không bị biến hình tức thời ta có thể thay đổi phương của liên kết thanh EF để không xảy ra trường hợp ba thanh đồng quy VD2 : Khảo sát cấu tạo hình học của hệ kết cấu sau 17 Điều kiện cần: Đây là hệ dàn không nối đất D = 21; M = 12 Thay vào (2.4) hệ đủ liên kết có thể BBH Điều kiện đủ: Dùng liên kết bộ đôi để phát triển các miếng cứng ta được các miếng cứng (I); (II); (III) như trên hình Ba miếng cứng (I); (II); (III) liên kết với nhau bằng các khớp (1,2); (1,3) và (2,3) không thẳng hàng nên ba miếng cứng (I); (II); (III) là một miếng cứng.Hai điểm B và C được liên kết vào miếng cứng trên bằng các bộ đôi. Kết luận: hệ đã cho đủ liên kết, bất biến hình. 18 Bài tập: xét cấu tạo hình học cho các hệ sau. 19
File đính kèm:
 bai_giang_co_hoc_ket_cau_1_chuong_2_phan_tich_cau_tao_hinh_h.pptx
bai_giang_co_hoc_ket_cau_1_chuong_2_phan_tich_cau_tao_hinh_h.pptx

