Bài giảng Toán rời rạc & Lý thuyết đồ thị - Chương 4: Các khái niệm về đồ thị
Định nghĩa 1.
Đơn đồ thị vô hướng G = (V,E) bao gồm V là tập các đỉnh, và E là tập các cặp
không có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh.
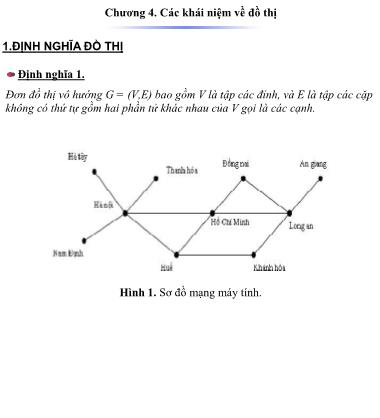
Hình 1. Sơ đồ mạng máy tính.Định nghĩa 2.
Đa đồ thị vô hướng G= (V, E) bao gồm V là tập các đỉnh, và E là tập các cặp
không có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh. Hai cạnh e1
và e2 được gọi là cạnh lặp nếu chúng cùng tương ứng với một cặp đỉnh.
Bạn đang xem tài liệu "Bài giảng Toán rời rạc & Lý thuyết đồ thị - Chương 4: Các khái niệm về đồ thị", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Toán rời rạc & Lý thuyết đồ thị - Chương 4: Các khái niệm về đồ thị
Chương 4. Các khái niệm về đồ thị
1.ĐỊNH NGHĨA ĐỒ THỊ
Định nghĩa 1.
Đơn đồ thị vô hướng G = (V,E) bao gồm V là tập các đỉnh, và E là tập các cặp
không có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh.
Hình 1. Sơ đồ mạng máy tính.
Định nghĩa 2.
Đa đồ thị vô hướng G= (V, E) bao gồm V là tập các đỉnh, và E là tập các cặp
không có thứ tự gồm hai phần tử khác nhau của V gọi là các cạnh. Hai cạnh e1
và e2 được gọi là cạnh lặp nếu chúng cùng tương ứng với một cặp đỉnh.
Hình 2. Sơ đồ mạng máy tính với đa kênh thoại.
Định nghĩa 3.
Đơn đồ thị có hướng G = (V, E) bao gồm V là tập các đỉnh và E là tập các cặp
có thứ tự gồm hai phần tử khác nhau của V gọi là các cung.
Hình 4. Mạng máy tính với kênh thoại một chiều
2. CÁC THUẬT NGỮ CƠ BẢN
Định nghĩa 1.
Hai đỉnh u và v của đồ thị vô hướng G được gọi là kề nhau nếu (u,v) là cạnh
của đồ thị G. Nếu e = (u, v) là cạnh của đồ thị ta nói cạnh này là liên thuộc với
hai đỉnh u và v, hoặc cũng nói là nối đỉnh u và đỉnh v, đồng thời các đỉnh u và
v sẽ được gọi là các đỉnh đầu của cạnh (u, v).
Định nghĩa 2.
Ta gọi bậc của đỉnh v trong đồ thị vô hướng là số cạnh liên thuộc với nó và sẽ
ký hiệu là deg(v).
deg(a) = 1, deg(b) = 4, deg(c) = 4, deg(f) = 3,
deg(d) = 1, deg(e) = 3, deg(g) = 0
Đỉnh bậc 0 gọi là đỉnh cô lập. Đỉnh bậc 1 được gọi là đỉnh treo. Trong ví dụ
trên đỉnh g là đỉnh cô lập, a và d là các đỉnh treo. Bậc của đỉnh có tính chất sau:
Định lý 1. Giả sử G = (V, E) là đồ thị vô hướng với |E| cạnh. Khi đó tổng
bậc của tất cả các đỉnh bằng hai lần số cạnh.
v
vE )deg(||2
Hệ quả. Trong đồ thị vô hướng, số đỉnh bậc lẻ (nghĩa là có bậc là số lẻ) là
một số chẵn.
Định nghĩa 3.
Nếu e = (u, v) là cung của đồ thị có hướng G thì ta nói hai đỉnh u và v là kề
nhau, và nói cung (u, v) nối đỉnh u với đỉnh v hoặc cũng nói cung này là đi ra
khỏi đỉnh u và vào đỉnh v. Đỉnh u(v) sẽ được gọi là đỉnh đầu (cuối) của cung
(u,v).
Định nghĩa 4.
Ta gọi bán bậc ra (bán bậc vào) của đỉnh v trong đồ thị có hướng là số cung
của đồ thị đi ra khỏi nó (đi vào nó) và ký hiệu là deg+(v) (deg-(v))
deg-(a)=1, deg-(b)=2, deg-(c)=2, deg-(d)=2, deg-(e) = 2.
deg+(a)=3, deg+(b)=1, deg+(c)=1, deg+(d)=2, deg+(e)=2.
Định lý 2. Giả sử G = (V, E) là đồ thị có hướng. Khi đó
2|E| = deg+(v) + deg-(v)
3. ĐƯỜNG ĐI. CHU TRÌNH. ĐỒ THỊ LIÊN THÔNG
Định nghĩa 1.
Đường đi độ dài n từ đỉnh u đến đỉnh v, trong đó n là số nguyên dương, trên
đồ thị vô hướng G = (V, E) là dãy
x0, x1,, xn-1, xn
trong đó u = x0 , v = xn , (xi , xi+1) E, i = 0, 1, 2,, n-1.
Đường đi nói trên còn có thể biểu diễn dưới dạng dãy các cạnh:
(x0, x1), (x1, x2), , (xn-1, xn)
Đỉnh u gọi là đỉnh đầu, còn đỉnh v gọi là đỉnh cuối của đường đi. Đường đi có
đỉnh đầu trùng với đỉnh cuối (tức là u = v) được gọi là chu trình. Đường đi
hay chu trình được gọi là đơn nếu như không có cạnh nào bị lặp lại.
Định nghĩa 2.
Đường đi độ dài n từ đỉnh u đến đỉnh v, trong đó, n là số nguyên dương, trên
đồ thị có hướng G = (V, A) là dãy
x0, x1,, xn-1, xn
trong đó u = x0, v = xn, (xi, xi+1) E, i = 0, 1, 2,, n-1.
Đường đi nói trên còn có thể biểu diễn dưới dạng dãy các cung:
(x0, x1), (x1, x2), , (xn-1, xn)
Đỉnh u gọi là đỉnh đầu, còn đỉnh v gọi là đỉnh cuối của đường đi. Đường đi có
đỉnh đầu trùng với đỉnh cuối (tức là u = v) được gọi là chu trình. Đường đi
hay chu trình được gọi là đơn nếu như không có cung nào bị lặp lại.
Định nghĩa 3.
Đồ thị G = (V, E) được gọi là liên thông nếu luôn tìm được đường đi giữa hai
đỉnh bất kỳ của nó.
Ví dụ. Đồ thị gồm các đỉnh a,b,c,d,e,f,g là liên thông. Còn đồ thị H tạo ra từ
H1,H2,H3 là không liên thông.
Định nghĩa 4.
Ta gọi đồ thị con của đồ thị G = (V, E) là đồ thị H = (W, F), trong đó W V và
F E.
Trong trường hợp đồ thị là không liên thông, nó sẽ rã ra thành một số đồ thị
con liên thông đôi một không có đỉnh chung. Những đồ thị con liên thông như
vậy ta sẽ gọi là các thành phần liên thông của đồ thị.
Ví dụ. Đồ thị H trong hình trên gồm 3 thành phần liên thông H1, H2, H3.
4. MỘT SỐ DẠNG ĐỒ THỊ ĐẶC BIỆT
Đồ thị đầy đủ.
Đồ thị đầy đủ n đỉnh, ký hiệu bởi Kn, là đơn đồ thị vô hướng mà giữa hai đỉnh
bất kỳ của nó luôn có cạnh nối.
Các đồ thị K3, K4, K5 cho trong hình dưới đây.
Đồ thị đầy đủ Kn có tất cả n(n-1)/2 cạnh, nó là đơn đồ thị có nhiều cạnh nhất.
Đồ thị hai phía.
Đơn đồ thị G=(V,E) được gọi là hai phía nếu như tập đỉnh V của nó có thể
phân hoạch thành hai tập X và Y sao cho mỗi cạnh của đồ thị chỉ nối một đỉnh
nào đó trong X với một đỉnh nào đó trong Y. Khi đó ta sẽ sử dụng ký hiệu
G=(X Y, E) để chỉ đồ thị hai phía với tập đỉnh X Y.
Đồ thị hai phía đầy đủ.
Đồ thị hai phía G=(X Y, E) với X = m, Y = n được gọi là đồ thị hai
phía đầy đủ và ký hiệu là K2,3, K3,3, K3,4 được cho trong hình dưới.
Đồ thị phẳng.
Đồ thị được gọi là đồ thị phẳng nếu ta có thể vẽ nó trên mặt phẳng sao cho các
cạnh của nó không cắt nhau ngọai trừ ở đỉnh. Cách vẽ như vậy sẽ được gọi là
biểu diễn phẳng của đồ thị.
Thí dụ đồ thị K4 là phẳng, vì có thể vẽ nó trên mặt phẳng sao cho các cạnh của
nó không cắt nhau.
Đồ thị phẳng còn tìm được những ứng dụng quan trọng trong công nghệ chế
tạo mạch in.
Biểu diễn phẳng của đồ thị sẽ chia mặt phẳng ra thành các miền, trong đó có
thể có cả miền không bị chặn (miền vô hạn). Thí dụ, biểu diễn phẳng của đồ thị
cho trong hình 7 chia mặt phẳng ra thành 6 miền R1, R2,. . . .R6. (miền R6 là
miền vô hạn)
Euler đã chứng minh được rằng các cách biểu diễn phẳng khác nhau của một
đồ thị đều chia mặt phẳng ra thành cùng một số miền. Để chứng minh điều đó,
Euler đã tìm được mối liên hệ giữa số miền, số đỉnh và số cạnh của đồ thị
phẳng sau đây.
Định lý 3 (Công thức Euler). Giả sử G=(V,E) là đồ thị phẳng liên thông
với |V| đỉnh, |E| cạnh. Gọi |R| là số miền của mặt phẳng bị chia bởi biểu diễn
phẳng của G. Khi đó
|R| = |E|-|V| + 2
Có thể chứng minh định lý bằng qui nạp. Xét thí dụ minh hoạ cho áp dụng
công thức Euler.
Thí dụ. Cho G là đồ thị phẳng liên thông với 20 đỉnh, mỗi đỉnh đều có bậc là
3. Hỏi mặt phẳng bị chia làm bao nhiêu phần bởi biểu diễn phẳng của đồ thị G?
Giải. Do mỗi đỉnh của đồ thị đều có bậc là 3, nên tổng bậc của các đỉnh là
3x20=60. Từ đó suy ra số cạnh của đồ thị |E|=60/2=30. Vì vậy, theo công thức
Euler, số miền cần tìm là
|R|=30-20+2=12.
Định lý 4 (Công thức Euler tổng quát). Giả sử G=(V,E) là đồ thị phẳng
với |V| đỉnh, |E| cạnh. Gọi |R| là số miền của mặt phẳng bị chia bởi biểu diễn
phẳng của G. Khi đó
|R| = |E|-|V| + Số thành phần liên thông + 1
5. MA TRẬN KỀ. MA TRẬN TRỌNG SỐ CỦA ĐỒ THỊ.
Xét đơn đồ thị vô hướng G=(V,E), với tập đỉnh V= 1, 2,. . . ,n , tập cạnh E=
e1, e2,. . .,em . Ta gọi ma trận kề của đồ thị G là ma trận vuông.
A= ai,j : i,j=1, 2,. . . ,n
Với các phần tử được xác định theo qui tắc sau đây:
ai, j = 0, nếu (i,j) E và
ai,j = 1 , nếu (i,j) E, i, j=1, 2,. . .,n.
Ví dụ 1. Ma trận trận kề của đồ thị vô hướng cho trong hình 1 là:
1 2 3 4 5 6
1 0 1 1 0 0 0
2 1 0 1 0 1 0
3 1 1 0 1 0 0
4 0 0 1 0 1 1
5 0 1 0 1 0 1
6 0 0 0 1 1 0
Hình 1. Đồ thị vô hướng G và Đồ thị có hướng G1
Các tính chất của ma trận kề:
1) Rõ ràng ma trận kề của đồ thị vô hướng là ma trận đối xứng, tức là
a[i,j]=a[j,i], i,j=1,2,. . .,n.
ngược lại, mỗi (0,1)-ma trận đối xứng cấp n sẽ tương ứng, chính xác đến
cách đánh số đỉnh (còn nói là: chính xác đến đẳng cấu), với một đơn đồ thị
vô hướng n đỉnh.
2) Tổng các phần từ trên dòng i (cột j) của ma trận kề chính bằng bậc của
đỉnh i (đỉnh j).
Ma trận kề của đồ thị có hướng được định nghĩa một cách hoàn toàn tương tự.
Thí dụ 2. Đồ thị có hướng G1 cho trong hình 1 có ma trận kề là ma trận sau:
1 2 3 4 5 6
1 0 1 1 0 0 0
2 0 0 0 0 0 0
3 0 1 0 1 0 0
4 0 0 0 0 0 0
5 0 0 0 1 0 1
6 0 0 0 0 1 0
Lưu ý rằng ma trận kề của đồ thị có hướng không phải là ma trận đối xứng.
Chú ý: Trên đây chúng ta chỉ xét đơn đồ thị. Ma trận kề của đa đồ thị có thể
xây dựng hoàn toàn tương tự, chỉ khác là thay vì ghi 1 vào vị trí a[i,j] nếu (i,j)
là cạnh của đồ thị, chúng ta sẽ ghi k là số cạnh nối hai đỉnh i, j.
Trong rất nhiều vấn đề ứng dụng của lý thuyết đồ thị, mỗi cạnh e=(u,v) của đồ
thị được gán với một con số c(e) [còn viết là c(u,v)] gọi là trọng số của cạnh e.
Đồ thị trong trường hợp như vậy được gọi là đồ thị có trọng số. Trong trường
hợp đồ thị có trọng số, thay vì mà trận kề, để biểu diễn đồ thị ta sử dụng ma
trận trọng số.
C= {c[i,j], i,j=1, 2,. . .,n}
với
c[i,j]=c(i,j) nếu (i,j) E
c[i,j]= nếu (i,j) E
c[i,i]=0
trong đó số , tuỳ từng trường hợp cụ thể, có thể được đặt bằng một trong các
giá trị sau: 0, + , -
Ví dụ:
Hình 2: Đồ thị và ma trận trọng số tương ứng của nó
Ưu điểm lớn nhất của phương pháp biểu diễn đồ thị bằng ma trận kề (hoặc ma
trận trọng số) là để trả lời câu hỏi: Hai đỉnh u,v có kề nhau trên đồ thị hay
không, chúng ta chỉ phải thực hiện một phép kiểm tra phần tử A[u,v] của ma
trận có khác 0 hay không.
BÀI TẬP.
Bài 1: Vẽ đồ thị có 6 đỉnh trong đó
a) 3 đỉnh bậc 3 và 3 đỉnh bậc 1.
b) Bậc các đỉnh lần lượt là: 1,2,2,3,4,5.
c) Bậc các đỉnh lần lượt là: 2,2,4,4,4,4.
Bài 2: Tìm số cạnh và vẽ đồ thị mà mọi đỉnh của nó đều có bậc 3 và có
a) 4 đỉnh.
b) 5 đỉnh.
c) 6 đỉnh.
d) 8 đỉnh.
Bài 3: Tìm số đỉnh và vẽ đồ thị mà nó có
a) 12 cạnh và mọi đỉnh đều có bậc 2.
b) 15 cạnh, 3 đỉnh bậc 4 và các đỉnh còn lại bậc 3.
c) 6 cạnh và mọi đỉnh có bậc bằng nhau.
Bài 4: Một đồ thị có 19 cạnh, mỗi đỉnh đều có bậc >=3. Đồ thị này có tối đa
bao nhiêu đỉnh?
Bài 5: Biết rằng mọi đỉnh của một đồ thị đều có bậc bằng số lẻ p. CMR số cạnh
cua nó là bội số của p.
Bài 6: Có thể tồn tại một nhóm có 9 người, trong đó mỗi người cùng tuổi với
đúng 3 người khác trong nhóm hay không?
Bài 7: Một đơn đồ thị phẳng liên thông có 10 mặt, tất cả các đỉnh đều có bậc 4.
Tìm số đỉnh, số cạnh và vẽ đồ thị.
Bài 8: Đơn đồ thị phẳng liên thông có 9 đỉnh, bậc các đỉnh là 2,2,2,3,3,3,4,4,5.
Tìm số cạnh, số mặt và vẽ đồ thị.
File đính kèm:
 bai_giang_toan_roi_rac_ly_thuyet_do_thi_chuong_4_cac_khai_ni.pdf
bai_giang_toan_roi_rac_ly_thuyet_do_thi_chuong_4_cac_khai_ni.pdf

