Bài tập Giải tích 2

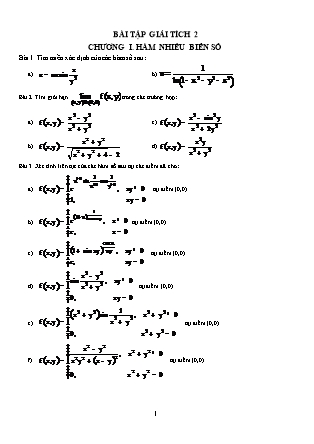
BÀI TẬP GIẢI TÍCH 2
CHƯƠNG I. HÀM NHIỀU BIẾN SỐ
Bài 1. Tìm miền xác định của các hàm số sau:
	b) 
Bài 2. Tìm giới hạn trong các trường hợp:
	c) 
	d) 
Bài 3. Xét tính liên tục của các hàm số sau tại các điểm đã cho:
 tại điểm (0,0)
 tại điểm (0,0)
 tại điểm (0,0)
 tại điểm (0,0)
 tại điểm (0,0).
 tại điểm (0,0)
 tại điểm (0,0)
Bài 4. Tìm các đạo hàm riêng của hàm số 
	b) 
Bài 5. Cho hàm số . Tính bằng định nghĩa. Hàm số có khả vi tại điểm O(0,0) hay không?
Bài 6. Chứng minh rằng hàm số liên tục taị điểm O(0,0), có cả hai đạo hàm riêng , nhưng không khả vi tại điểm này.
Bài 7. Khảo sát tính khả vi của hàm số tại điểm (0,0).
Bài 8. Cho hàm số . Tính .
Bài 9. Ứng dụng công thức số gia và vi phân toàn phần để tính gần đúng
	c) 
	d) 
Bài 10. Cho là hàm số xác định bởi hệ thức trong đó a, b là hằng số, F là hàm khả vi. Tìm biểu thức .
Bài 11. Giả sử là các hàm khả vi. Đặt và . Chứng minh rằng
	b) .
Bài 12. Cho hàm số xác định từ phương trình (trong đó là hàm khả vi theo . Chứng minh rằng .
Bài 13. Sử dụng quy tắc đạo hàm hàm ẩn để tính biết .
Bài 14. Sử dụng quy tắc đạo hàm hàm ẩn để tìm
 biết là hàm ẩn xác định từ ;
 biết là hàm ẩn xác định từ ;
 biết là hàm ẩn xác định từ 
Bài 15. Tìm các đạo hàm riêng cấp hai của các hàm số
	b) 	c) 
Bài 16. Tìm đạo hàm của u tại điểm A trong đó
 theo hướng và điểm A(1,2,-2). Tìm .
 theo hướng tại điểm A(1,3,0).
 với A (1,1,1) theo hướng , trong đó N(3,2,3).
Bài 17. 
Khai triển hàm số thành công thức Taylor trong lân cận điểm (1,-2).
Khai triển hàm số thành công thức Macloranh đến các số hạng cấp bốn. 
Bài 18. Tìm cực trị của hàm số sau
Bài 19. Tìm cực trị có điều kiện
 thỏa mãn điều kiện 
 thỏa mãn điều kiện 
 thỏa mãn điều kiện 
 thỏa mãn điều kiện 
 thỏa mãn điều kiện .
Bài 20. Tìm GTLN, GTNN của hàm số trên miền đóng D.
, trong đó D là với A(0,0), B(0,6), C(6,0)
Đáp án chương I.
1.a) trừ những điểm trên Ox; b) trừ gốc tọa độ O
2.a) Không tồn tại; 	b) 4;	c) Không tồn tại;	d) 0
3.a) Liên tục;	b) Không liên tục; c) liên tục;	d) không liên tục; e) Liên tục; f) không liên tục. 
g) không liên tục. 
4. a)	b) 
5. . Hàm số không khả vi tại (0,0).
7. Hàm số khả vi tại điểm (0,0).
8. .
9. a) 2,95	b) 1,0129	c) 2,0327	d) 1,08
10. 1
13. 
14. a) 	
 b) 	c) 
16. a) 	b) 	c) .
17. a)
 b) 
18. a) Cực đại 	b) Cực đại 	c) Cực tiểu 	
 d) Cực tiểu 	e) Cực tiểu; (0,0) không là cực trị
 f) Cực tiểu (1;1), (-1;-1); (0,0) không là cực trị	g) (1;0) không là cực trị.
 h) Cực đại ; (0, 0) không là cực trị.	i) là cực tiểu; (3;1) không là cực trị.
19. a) Cực tiểu (-1;0;1)	b) cực tiểu , cực đại 
 c) cực tiểu , cực đại 	d) cực đại (2;2;-1), cực tiểu (-2;-2;1).
 e) Cực đại (1;1;1)
20. a) 
 b) 
 c) 
 d) 
 e) .
CHƯƠNG II. TÍCH PHÂN BỘI
Bài 1. Tính tích phân kép sau trên miền D được chỉ ra
 với D được giới hạn bởi 	
 với D được giới hạn bởi .	
 với D được giới hạn bởi 	
 với D được giới hạn bởi 	
Bài 2. Đổi thứ tự lấy tích phân rồi tính các tích phân sau
	b) 	
Bài 3. Dùng phép đổi biến thích hợp, tính các tích phân sau
 trong đó D là hình giới hạn bời các đường thẳng .	
 trong đó D là miền nằm trong góc phần tư thứ nhất giới hạn bởi các đường thẳng y=x, y=3x và các hypebol xy=1, xy=3.	
Bài 4. Dùng công thức đổi biến chứng minh rằng
	b) 
Bài 5 Dùng đổi biến tọa độ cực tính các tích phân sau
trong đó D là miền nằm trong góc phần tư thứ nhất bị chặn bởi 2 đường tròn .	
;	
;	
Bài 6. Dùng tích phân hai lớp tính diện tích của các hình phẳng
Giới hạn bởi 	
Nằm trong cả hai đường tròn và 	
Bị chặn bởi các đường cong 	
Giới hạn bởi đường cong (L): 	
Giới hạn bởi đường cong (L): 	
Bài 7. Tính diện tích của mặt cong
Là giao của các mặt trụ 	
Là phần mặt cầu nằm trong hình trụ 	
Là phần mặt nằm trong hình trụ 	
Là phần mặt paraboloid nằm trên miền trong góc phần tư thứ nhất (của mặt Oxy) giới hạn bởi các đường và .	
Bài 8. Tính thể tích V của vật thể
Giới hạn bởi mặt trụ và mặt cầu 	
Xác định bởi các bất đẳng thức 
Trên mặt nón và nằm dưới mặt cầu 	
Trên mặt nón và nằm dưới mặt cầu 	
Bị chặn bởi các paraboloid và 	
Bị chặn bởi paraboloid và mặt phẳng 	
Giới hạn bởi các mặt cong và 	
Giới hạn bởi các mặt có phương trình 	
Bị chặn bởi hai hình trụ và 	
Bài 9. Tính thể tích của vật thể giới hạn bởi mặt đóng
	. 
Bài 10. Tính các tích phân bội ba sau
 trong đó V là miền được giới hạn bởi mặt phẳng 	
 trong đó V là miền được giới hạn bởi 	
	0
 trong đó V giới hạn bởi (Oxy) và hai nửa mặt cầu và 	
 trong đó V là vật thể bị chặn bởi (Oxy) và mặt nón 	
 trong đó V là vật thể nằm trong mặt cầu và trên mặt nón 	
 trong đó V là vật thể giới hạn bới mặt trụ 
	;
 trong đó V là vật thể giới hạn bới 	0
; 
CHƯƠNG III. TÍCH PHÂN ĐƯỜNG VÀ TÍCH PHÂN MẶT
Bài 1. Tính tích phân đường loại một sau
 với L là đường 	
 với L là đoạn thẳng nằm giữa hai điểm A(0;-2) và B(4;0)	
 với L là đường tròn 	
 với L là nửa đường tròn chạy từ đến 
với L là đường 	
Bài 2. Tính các tích phân đường loại hai sau:
 trong đó L là đường gấp khúc OAB với O(0,0); A(2,0); B(3,2).	
 trong đó L là cung nối O(0,0) với A(1,1) theo đường
i)	ii) 	iii) gấp khúc OBA với B(0,1)
Bài 3. Chứng minh rằng tích phân không phụ thuộc vào đường lấy tích phân trong miền đơn liên, liên thông . Tính I nếu AB là đường bất kỳ không cắt Ox đi từ A(0,0) tới B(1,1).	
Bài 4. Chứng minh rằng tích phân không phụ thuộc vào đường lấy tích phân. Tính I nếu C là đường bất kỳ nối A(-1,0) tới (5,1).	
Bài 5. Tính tích phân sau theo hai cách: trực tiếp và dùng công thức Green:
 với L là hình chữ nhật OABC với O(0,0), A(2,0), B(2,3), C(0,3)	
 với L là cung nối A(0,-a) đến B(0,a) trong đó a>0.	
Bài 6. Dùng công thức Green tính các tích phân sau
 trong đó C là đường tròn lấy theo chiều ngược kim đồng hồ.	
 với L là cung tròn lấy theo chiều tăng của t: .	
 với L là nửa đường tròn đi từ O(0,0) đến A(0,2).	
 trong đó L là đường tròn lấy theo chiều dương.	
 với L là đường cong chạy từ đến O(0,0).	
Bài 7. Tính các tích phân mặt loại một sau:
 với S là phần mặt paraboloid nằm dưới mặt phẳng 	
 trong đó S là phần mặt cầu 	
 với S là phần mặt trụ nằm giữa hai mặt phẳng và mặt phẳng .	
Tính tích phân mặt: trong đó S là phần mặt nón tròn xoay bị chắn giữa hai mặt trụ và .	
Bài 8. Tính các tích phân mặt loại hai sau:
 trong đó S là phía ngoài của mặt nón (không kể đáy)	
 trong đó S là phần mặt cầu nằm ở góc phần tám thứ nhất và hướng ra ngoài.	
 trong đó S là mặt xung quanh của tứ diện giới hạn bới các mặt phẳng và mặt và hướng ra phía ngoài.	
 trong đó S là phía ngoài của mặt cầu .	
Bài 9. Dùng định lý Stokes tính các tích phân sau:
 trong đó L là elip giao bởi mặt trụ và mặt phẳng (a>0) có hướng ngược chiều kim đồng hồ nếu nhìn từ phía dương của trục Oz nhìn xuống. 	
 trong đó L là đường tròn lấy theo chiều ngược chiều kim đồng hồ khi nhìn từ bên trên.	
 trong đó L là đường cong có hướng ngược chiều kim đồng hồ khi nhìn từ bên trên.	
Bài 10. Dùng công thức Ostrogradski – Gauss đề tính các tích phân sau:
 với S là phía ngoài của nửa mặt cầu (không kể phần hình tròn nằm trong mặt phẳng Oxy).	
 có S là mặt xung quanh của khối trụ (không kể hai đáy) hướng ra ngoài.	
 có S là mặt xung quanh của khối trụ (không kể hai đáy) hướng ra ngoài.	
 với S là mặt nón không kể đáy và hướng ra ngoài.	
 có S là mặt cầu hướng ra ngoài.	
 có S là mặt cầu hướng ra ngoài.	0
 trong đó S là mặt ngoài của vật thể V giới hạn bởi: ;
 có S là phía ngoài của mặt nằm trong góc phần tám thứ nhất tạo nên bởi mặt và các mặt phẳng tọa độ x=0,y=0,z=0.	
CHƯƠNG IV: PHƯƠNG TRÌNH VI PHÂN
Bài 1. Giải các phương trình tách biến sau:
Bài 2. Giải các phương trình vi phân đẳng cấp (thuần nhất) sau:
Bài 3. Giải các phương trình đưa được về phương trình thuần nhất sau:
Bài 4. Giải các phương trình vi phân tuyến tính sau:
Bài 5. Giải các phương trình vi phân Bernoulli:
Bài 6. Giải các PTVP toàn phần sau:
Bài 7. Giải các PTVP dùng thừa số tích phân sau:
Bài 8. Tìm nghiệm riêng của PTVP sau thỏa mãn điều kiện đã cho:
Bài 9. Giải các PTVP sau bằng phương pháp hệ số bất định:
Bài 10. Giải các PTVP sau bằng phương pháp biến thiên hằng số Lagrange:
Bài 11. Giải các phương trình Euler sau:
Bài 12. Giải phương trình bằng phép đổi hàm 
Đáp số. 
Bài 13. Giải các hệ PTVP sau:
	b) 	c) 
	b) 	c)