Nghiên cứu ứng suất kéo của cọc bê tông đóng trong nền một lớp đáy cọc tựa trên nền cứng ngay sau khi va chạm

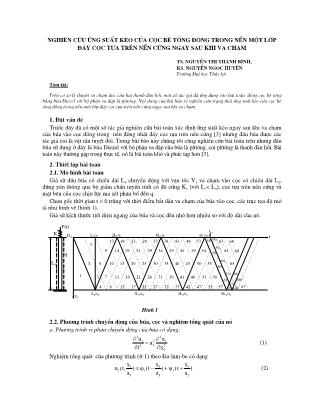
nghiên cứu ứng suất kéo của cọc bê tông đóng trong nền một lớp 
đáy cọc tựa trên nền cứng ngay sau khi va chạm 
 TS. Nguyễn Thị Thanh Bình, 
 KS. Nguyễn Ngọc Huyên 
 Trường Đại học Thủy lợi 
Tóm tắt: 
Trên cơ sở lý thuyết va chạm dọc của hai thanh đàn hồi, một số tác giả đã ứng dụng vào bài toán đóng cọc bê tông 
bằng búa Diezel với bộ phận va đập là pittông. Nội dung của bài báo sẽ nghiên cứu trạng thái ứng suất kéo của cọc bê 
tông đóng trong nền một lớp đáy cọc tựa trên nền cứng ngay sau khi va chạm. 
1. Đặt vấn đề 
Trước đây đã có một số tác giả nghiên cứu bài toán xác định ứng suất kéo ngay sau khi va chạm 
của búa vào cọc đóng trong nền đồng nhất đáy cọc tựa trên nền cứng [3] nhưng đầu búa được các 
tác giả coi là vật rắn tuyệt đối. Trong bài báo này chúng tôi cũng nghiên cứu bài toán trên nhưng đầu 
búa sử dụng ở đây là búa Diezel với bộ phận va đập của búa là píttông, coi píttông là thanh đàn hồi. Bài 
toán này thường gặp trong thực tế, nó là bài toán khó và phức tạp hơn [3]. 
2. Thiết lập bài toán 
2.1. Mô hình bài toán 
Giả sử đầu búa có chiều dài L1 chuyển động với vận tốc V1 va chạm vào cọc có chiều dài L2, 
đứng yên thông qua bộ giảm chấn tuyến tính có độ cứng K1 (với L1< L2), cọc tựa trên nền cứng và 
mặt bên của cọc chịu lực ma sát phân bố đều q. 
Chọn gốc thời gian t = 0 trùng với thời điểm bắt đầu va chạm của búa vào cọc, các trục tọa độ mô 
tả như hình vẽ (hình 1). 
Giả sử kích thước tiết diện ngang của búa và cọc đều nhỏ hơn nhiều so với độ dài của nó. 
2.2. Phương trình chuyển động của búa, cọc và nghiệm tổng quát của nó 
a. Phương trình vi phân chuyển động của búa có dạng: 
2 2
21 1
12 2
1
u u
a
t x
 
 
 (1) 
Nghiệm tổng quát của phương trình (4-1) theo Đa-lăm-be có dạng 
 1 1 11 1 1
1 1 1
x x x
u (t, ) (t ) (t )
a a a
  (2) 
t 
x2 
 L2 
K 
q 
O2 
1 
L2/a2 3L2/a2 5L2/a2 8L2/a2 
2L2/a2 4L2/a2 6L2/a2 L2/a2 
2 6 
5 
4 
3 7 
8 
9 
13 
10 
11 
12 
18 
14 
15 
16 
17 
19 
20 
21 
22 
23 
24 
25 
26 
27 
28 
29 
30 
31 
32 
33 
34 
35 
36 
37 
38 
39 
40 
41 
42 
43 
44 
45 
46 
47 
48 
49 
50 
51 
52 
58 
59 
60 
61 
62 
68 
69 
53 
54 
55 
56 
57 
63 
64 
65 
66a 
67 
58a 
59a 
60a 
61a 
62a 
62b 
66b 
tvc 
P(t) 
Hình 1 
b. Phương trình vi phân chuyển động của cọc có dạng: 
2 2
22 2
2 12 2
2
u u
a K
t x
  
  
 (3) 
Nghiệm tổng quát của (3) theo Đa-lăm-be: 
ở miền 2, 5 có dạng: 22 2 12 2 2 1 2 2
2 2
x x K
u (t, ) (t ) x K a tx
a a 2
 (4a) 
ở miền 3, 6, 9, 13 có dạng: 22 2 12 2 2 2
2 2
x x K
u (t, ) (t ) (L x )
a a 2
 (4b) 
ở miền còn lại có dạng: 22 2 2 12 2 2 2 2
2 2 2
x x x K
u (t, ) (t ) (t ) (L x )
a a a 2
  (4c) 
Với n = 1, 2 là số thứ tự biểu thị búa và cọc; 
1
2 2
r.q
K
E F
 ; nn
n
E
a 
 là vận tốc truyền sóng trong piston búa và cọc; 
q - Lực cản ma sát mặt bên cọc; 
En, n là modun đàn hồi và khối lượng riêng vật liệu làm búa và cọc; 
Un là hàm dịch chuyển của búa và cọc. 
2.3. Điều kiện của bài toán 
a. Điều kiện đầu của bài toán 
Với t = 0 ta có: 1 1
u
V
t


; 1
1
u
0
x


; 2
u
0
t


; 2
2
u
0
x


 (5) 
b. Điều kiện biên của bài toán 
Tại tiết diện x1 = 0 và x2 = 0 có dạng: 
1 2
1 1 2 2 1 2
1 2
u u
E F E F C( u u )
x x
 
 
 (6a) 
Tại tiết diện x1 = L1 thì: 
1
1
U
0
x


 (6b) 
Tại tiết diện x2 = L2 thì: 
2U 0
t


 (6c) 
Khi kết thúc va chạm: P(t) = 0 (6d) 
3. Xác định các hàm sóng truyền trong cọc 
Theo [3] đã xác định được lực nén P(t) của búa lên đầu cọc và các hàm sóng trong cọc trong thời 
gian va chạm. 
Dưới đây ta sử dụng một phần kết quả đó để xác định các hàm sóng truyền trong cọc ngay sau 
khi va chạm và tính ứng suất trong cọc. 
Giả sử thời điểm kết thúc va chạm ở trong khoảng 2 2
2 2
12L 13L
;
2a 2a
 và ta gọi thời điểm kết thúc va 
chạm là tvc. Sơ đồ bài toán như trên hình vẽ (hình 1). 
Ta có sóng thuận ở các miền 58, 59, 60, 61, 62 có dạng: 
2 32192 2 2 221 2 222 2
2 233 234 220
2 2 2 2 2
4 5 6 7 8223 225 226 2272 224 2 2 2 2
2 2 2 2 2
9 10228 229 2302 2 2
2 2
cx x x c x c x
(t ) c (t ) c c (t ) (t ) (t )
a a a 2 a 3 a
c c c cx c x x x x
(t ) (t ) (t ) (t ) (t )
4 a 5 a 6 a 7 a 8 a
c c cx x x
(t ) (t ) (t
9 a 10 a 11
2
2
x
(t )
a11 12231 2
2 2
c x
) (t ) e
a 12 a
 (7) 
Sóng phản ở miền 62, 62a, 66a có dạng: 
22192 2 2 2 2 221 2 2
2 233 234 220
2 2 2 2
3 4 5 6223 225222 2 2 2 2 224 2 2 2 2
2 2 2 2
7 8226 227 2282 2 2 2 2 2
2 2 2
cx x L x L c x L
(t ) c (t ) c c (t ) (t )
a a a 2 a
c cc x L x L c x L x L
(t ) (t ) (t ) (t )
3 a 4 a 5 a 6 a
c c cx L x L x L
(t ) (t ) (t
7 a 8 a 9 a
  
2 2
2
9 10229 2 2
2
x L
(t )
a11 12230 2312 2 2 2
2 2
c x L
) (t )
10 a
c cx L x L
(t ) (t ) e
11 a 12 a
 (8) 
Sóng phản ở miền 58a có dạng: 
2115 1172 2 2 2 2 2 2
2 125 126 116
2 2 2 2
3 4 5118 119 1202 2 2 2 2 2
2 2 2
(
6 7 8120 1232 2 122 2 2 2 2
2 2 2
c cx x 2L x 2L x 2L
(t ) c (t ) c c (t ) (t )
a a a 2 a
c c cx 2L x 2L x 2L
(t ) (t ) (t )
3 a 4 a 5 a
c cx 2L c x 2L x 2L
(t ) (t ) (t ) e
6 a 7 a 8 a
  
2 2
2
x 2L
t )
a
 (9) 
Sóng phản ở miền 59a, 63 có dạng: 
2138 1402 2 2 2 2 2 2
2 149 150 139
2 2 2 2
3 4 5 6143141 2 2 142 2 2 2 2 144 2 2
2 2 2 2
7 8145 146 1472 2 2 2
2 2
c cx x 2L x 2L x 2L
(t ) c (t ) c c (t ) (t )
a a a 2 a
cc x 2L c x 2L x 2L c x 2L
(t ) (t ) (t ) (t )
3 a 4 a 5 a 6 a
c c cx 2L x 2L
(t ) (t ) (
7 a 8 a 9
  
2 2
2
x 2L
(t )
a92 2
2
x 2L
t ) e
a
 (10) 
Sóng phản ở miền 60a, 64 và miền 68 có dạng: 
2163 1652 2 2 2 2 2 2
2 175 176 164
2 2 2 2
3 4 5 6166 167 168 1692 2 2 2 2 2 2 2
2 2 2 2
7 8170 171 1722 2 2 2
2 2
c cx x 2L x 2L x 2L
(t ) c (t ) c c (t ) (t )
a a a 2 a
c c c cx 2L x 2L x 2L x 2L
(t ) (t ) (t ) (t )
3 a 4 a 5 a 6 a
c c cx 2L x 2L
(t ) (t ) (
7 a 8 a 9
  
2 2
2
x 2L
(t )
a9 101732 2 2 2
2 2
cx 2L x 2L
t ) (t ) e
a 10 a
 (11) 
Sóng phản ở miền 61a, 65, 69 có dạng: 
2 3190 192 1932 2 2 2 2 2 2 2 2
2 203 204 191
2 2 2 2 2
4 5 6 7194 195 196 1972 2 2 2 2 2 2 2
2 2 2 2
8198 1992 2
2
c c cx x 2L x 2L x 2L x 2L
(t ) c (t ) c c (t ) (t ) (t )
a a a 2 a 3 a
c c c cx 2L x 2L x 2L x 2L
(t ) (t ) (t ) (t )
4 a 5 a 6 a 7 a
c cx 2L
(t ) (
8 a 9
  
2 2
2
x 2L
(t )
a9 10 11200 2012 2 2 2 2 2
2 2 2
c cx 2L x 2L x 2L
t ) (t ) (t ) e
a 10 a 11 a
 (12) 
Sau khi kết thúc va chạm ta có: 
2
2
2 x 0
U
0
x


Suy ra: 
2
2
2 2 1 2
2 2 2x 0
U 1 1
(t) (t) K L 0
x a a

  

; Ta có: 2 2 1 2 2(t) (t) K a L  (13) 
Ta có sóng thuận ở các miền 58a, 59a, 60a, 61a, 62a, 62b có dạng: 
2 3 4115 117 118 1192 2 2 2 2 2 2 2 2 2 2
2 125 126 116
2 2 2 2 2 2
(
5 6 7 8120 120 1232 2 2 2 122 2 2 2 2
2 2 2 2
c c c cx x 2L x 2L x 2L x 2L x 2L
(t ) c (t ) c c (t ) (t ) (t ) (t )
a a a 2 a 3 a 4 a
c c cx 2L x 2L c x 2L x 2L
(t ) (t ) (t ) (t ) e
5 a 6 a 7 a 8 a
2 2
2
x 2L
t )
a
1 2 2Ka L
 (14) 
Từ điều kiện biên ta có sóng phản ở miền 62b, 66b, 70b có dạng: 
2 3 4115 117 118 1192 2 2 2 2 2 2 2 2 2 2
2 125 126 116
2 2 2 2 2 2
(
5 6 7 8120 120 1232 2 2 2 122 2 2 2 2
2 2 2 2
c c c cx x 4L x 4L x 4L x 4L x 4L
(t ) c (t ) c c (t ) (t ) (t ) (t )
a a a 2 a 3 a 4 a
c c cx 4L x 4L c x 4L x 4L
(t ) (t ) (t ) (t ) e
5 a 6 a 7 a 8 a
  
2 2
2
x 4L
t )
a
1 2 2Ka L
 (15) 
Sóng thuận ở các miền 63, 64, 65, 66a, 66b, 67 có dạng: 
2 3 4138 1402 2 2 2 2 2 2 141 2 2 142 2 2
2 149 150 139
2 2 2 2 2 2
5
6 7 8143 145 146 1472 2 144 2 2 2 2 2 2
2 2 2 2
c cx x 2L x 2L x 2L c x 2L c x 2L
(t ) c (t ) c c (t ) (t ) (t ) (t )
a a a 2 a 3 a 4 a
c c c cx 2L c x 2L x 2L x 2L
(t (t ) (t ) (t ) (t
5 a 6 a 7 a 8 a 9
2 2
2
x 2L
(t )
a92 2
1 2 2
2
x 2L
) e KL a
a
 (16) 
Từ điều kiện biên ta có sóng phản ở miền 67, 71: 
2 3 4138 1402 2 2 2 2 2 2 141 2 2 142 2 2
2 149 150 139
2 2 2 2 2 2
5 6 7 8143 145 146 1472 2 144 2 2 2 2 2 2
2 2 2 2
c cx x 4L x 4L x 4L c x 4L c x 4L
(t ) c (t ) c c (t ) (t ) (t ) (t )
a a a 2 a 3 a 4 a
c c c cx 4L c x 4L x 4L x 4L
(t ) (t ) (t ) (t ) (
5 a 6 a 7 a 8 a 9
  
2 2
2
x 4L
(t )
a92 2
1 2 2
2
x 4L
t ) e KL a
a
 (17) 
4. Trạng thái ứng suất trong cọc 
Theo định luật Huc ta có công thức tính ứng suất trong cọc là: 
 2 2 2 22 2 2 1 2 2 2
2 2 2 2
u E x x
E (t ) (t ) K a L x
x a a a
 
   
 
 (18) 
Thay các hàm sóng tìm được vào (18) ta có: 
ứng suất trong cọc ở miền 58a có dạng: 
2115 1172 2 2 2 2 2 2
125 126 116
2 2 2 2
3 4 5118 119 1202 2 2 2 2 2
2 2 2
(t
6 7 8120 1232 2 122 2 2 2 2
2 2 2
c cE x 2L x 2L x 2L
c (t ) c c (t ) (t )
a a a 2 a
c c cx 2L x 2L x 2L
(t ) (t ) (t )
3 a 4 a 5 a
c cx 2L c x 2L x 2L
(t ) (t ) (t ) e
6 a 7 a 8 a
 
2 2
2
2
x 2L
)
a
2115 1172 2 2 2 2 2
125 126 116
2 2 2
3 4 5118 119 1202 2 2 2 2 2
2 2 2
6 7120 2 2 122 2 2
2 2
x
(t
8123 2 2
2
c cx 2L x 2L x 2L
c (t ) c c (t ) (t )
a a 2 a
c c cx 2L x 2L x 2L
(t ) (t ) (t )
3 a 4 a 5 a
c x 2L c x 2L
(t ) (t )
6 a 7 a
c x 2L
(t ) e
8 a
2
2
2L
)
a
1 2 2 1 2 2 2K a L K a L x
Ta có ứng suất trong cọc ở miền 59a có dạng: 
2115 1172 2 2 2 2 2 2
125 126 116
2 2 2 2
3 4 5118 119 1202 2 2 2 2 2
2 2 2
(t
6 7 8120 1232 2 122 2 2 2 2
2 2 2
c cE x 2L x 2L x 2L
c (t ) c c (t ) (t )
a a a 2 a
c c cx 2L x 2L x 2L
(t ) (t ) (t )
3 a 4 a 5 a
c cx 2L c x 2L x 2L
(t ) (t ) (t ) e
6 a 7 a 8 a
 
2 2
2
x 2L
)
a
2138 1402 2 2 2 2 2
149 150 139
2 2 2
3 4 5 6143141 2 2 142 2 2 2 2 144 2 2
2 2 2 2
7 8145 146 1472 2 2 2
2 2
c cx 2L x 2L x 2L
c (t ) c c (t ) (t )
a a 2 a
cc x 2L c x 2L x 2L c x 2L
(t ) (t ) (t ) (t )
3 a 4 a 5 a 6 a
c c cx 2L x 2L x
(t ) (t ) (t
7 a 8 a 9
2 2
2
x 2L
(t )
a92 2
2
1 2 2 1 2 2 2
2L
) e
a
K a L K a L x
. 
5. Tính toán với số liệu cụ thể 
5.1. Búa: Búa Điêzen đầu búa có kích thước 30x30x287cm, khối lượng riêng 1 = 0,00784kg/cm
3, 
môđun đàn hồi E1= 2,1.10
7 N/cm2. 
Hình 2: Đồ thị ứng suất tại thời 
điểm t = 0,0148s 
Hình 3: Đồ thị ứng suất tại 
thời điểm t = 0,0150s 
Hình 4: Đồ thị ứng suất tại 
thời điểm t = 0,0152s 
5.2. Cọc: Cọc bê tông mác M300 có kích thước 40x40x800 cm, khối lượng riêng 1 = 0,0024kg/cm
3, 
môđun đàn hồi E2= 3,11.10
6 N/cm2. 
5.3. Đệm: Đệm giảm chấn có độ cứng 1,2114.105N/cm. 
5.4. Đất nền: Đất nền một lớp với lực ma sát mặt bên phân bố đều: q = 2,5 N/cm2, đáy cọc gặp 
lớp đá tảng. 
Với số liệu trên, từ những công thức tính lực nén và ứng suất trong cọc đã thiết lập được, sử dụng 
ngôn ngữ lập trình Matlab, viết chương trình chạy trên máy vi tính. Thời gian kết thúc va chạm tvc = 
0,0141s. Tính toán ứng suất trong cọc ngay sau khi va chạm kết thúc tại ba thời điểm: t1 = 0,0148s; 
t2 = 0,0150s; t3 = 0,0152s. 
5.5. Nhận xét 
Từ các đồ thị ta có một số nhận xét sau: 
 - Tại thời điểm t = 0,0148s thì trong cọc 
xuất hiện cả ứng suất nén và ứng suất kéo, ứng 
suất kéo lớn nhất  = – 38,4425 N/cm2 xuất 
hiện tại tiết diện x2 = 230,5223 cm. 
- Tại thời điểm t = 0,0150 s thì trong cọc 
xuất hiện cả ứng suất nén và ứng suất kéo, ứng 
suất kéo lớn nhất  = – 74,5072 N/cm2 xuất 
hiện tại tiết diện x2 = 296,3858cm. 
- Tại thời điểm t = 0,0152s ứng suất kéo 
lớn nhất trong cọc  = – 100,177 N/cm2 xuất 
hiện tại tiết diện x2 = 378,7152cm. Tại thời 
điểm này cọc có khả năng bị vỡ (do ứng suất 
kéo > ứng suất kéo giới hạn). 
6. Kết luận 
Mô hình bài toán này tổng quát hơn so với mô hình một số bài toán đã được nghiên cứu.Trong 
bài báo này búa được coi là thanh đàn hồi nên khi giải bài toán này sẽ khó khăn và phức tạp hơn. 
Qua tính toán với số liệu cụ thể cho thấy kết quả nhận được là sát với thực tế và phù hợp với kết 
quả ở [5]. 
Trong bài toán này do ảnh hưởng của ma sát mặt bên nên ứng suất kéo cực đại ngay sau khi va 
chạm thường xảy ra ở gần đầu cọc. 
 (Công trình này được sự tài trợ của Viện KH&CN Việt Nam – Bộ KH&CN) 
 Tài liệu tham khảo 
[1] Nguyễn Thúc An, Lý thuyết va chạm dọc của thanh và ứng dụng vào bài toán đóng cọc, 
Trường Đại học Thủy lợi. 1991 
[2] Nguyễn Thúc An, Nguyễn Thị Thanh Bình, Bùi Quang Nhung, Trạng thái ứng suất của cọc 
đóng trong nền đồng nhất đáy cọc tựa trên nền cứng ngay sau khi va chạm. Tuyển tập hội nghị 
khoa học toàn quốc về cơ học kỹ thuật 10/2001. 
[3] Nguyễn Đăng Cường, Nguyễn Thị Thanh Bình, Nguyễn Ngọc Huyên, áp dụng lí thuyết va 
chạm dọc của hai thanh đàn hồi vào bài toán xác định ứng suất của cọc đóng trong nền đồng nhất 
đáy cọc tựa trên nền cứng, Tạp chí Khoa học và Công nghệ 41 (2). 2003. 
[4] Nguyễn Thị Thanh Bình, Nguyễn Ngọc Huyên, áp dụng lí thuyết va chạm dọc của hai thanh 
đàn hồi để xác định trạng thái ứng suất của cọc đóng trong nền đồng nhất, đáy cọc tựa trên nền 
cứng, Tuyển tập các báo cáo hội nghị cơ học toàn quốc kỷ niệm 25 năm thành lập Viện Cơ học, T1. 
4/2004. 
[5] Cung Nhật Minh, Diệp Vạn Ninh, Lưu Hưng Lục, Thí nghiệm và kiểm tra chất lượng cọc, 
NXB Xây Dựng 1999. 
[6] Nguyễn Phùng Quang, Matlab and Simulink, NXB Khoa học và Kỹ thuật. 2004 
Abstract 
Based on longitudinal shock of two elastic bars theory, some authors applied concrete pile- driven problem by Diesel 
hammer with knocked-section is piston. This paper studied tension stress of the concrete pile which was driven in one 
layer, pile’s bottom placed a hard foundation at shock – finish.