Giáo trình Lý thuyết điều khiển tự động 1

Giáo trình Lý thuyết điều khiển tự động 1 
CHƯƠNG 1 : MÔ TẢ MỘT HỆ THỐNG ĐIỀU KHIỂN TỰ ĐỘNG 
1.1 Các khái niệm cơ bản 
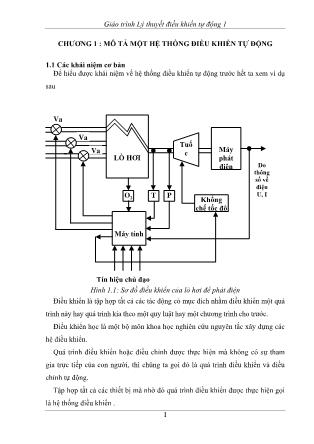
Để hiểu được khái niệm về hệ thống điều khiển tự động trước hết ta xem ví dụ 
sau 
Tuố
c 
bi
Máy 
phát 
điện Đo 
thông 
số về 
điện 
U, IO2 T P
Máy tính
Khống 
chế tốc độ 
Va
Va
Va
LÒ HƠI
Tín hiệu chủ đạo
Hình 1.1: Sơ đồ điều khiển của lò hơi để phát điện 
Điều khiển là tập hợp tất cả các tác động có mục đích nhằm điều khiển một quá 
trình này hay quá trình kia theo một quy luật hay một chương trình cho trước. 
Điều khiển học là một bộ môn khoa học nghiên cứu nguyên tắc xây dựng các 
hệ điều khiển. 
Quá trình điều khiển hoặc điều chỉnh được thực hiện mà không có sự tham 
gia trực tiếp của con người, thì chúng ta gọi đó là quá trình điều khiển và điều 
chỉnh tự động. 
Tập hợp tất cả các thiết bị mà nhờ đó quá trình điều khiển được thực hiện gọi 
là hệ thống điều khiển . 
 1
Giáo trình Lý thuyết điều khiển tự động 1 
Tập hợp tất cả các thiết bị kỹ thuật, đảm bảo ĐK hoặc ĐC tự động một quá 
trình nào đó được gọi là hệ thống ĐK hoặc ĐC tự động (đôi khi gọi tắt là hệ 
thống tự động – HTTĐ). 
1.2 Các phần tử cơ bản của hệ thống điều khiển tự động 
Đối tượng điều khiển (Object), Thiết bị điều khiển (Controller ), Thiết bị đo 
lường (Measuring device). 
- Sơ đồ tổng quát 
 2
OC
M
- 
z(t) 
u(t) e(t) x(t) y(t) 
Hình 1.2: Sơ đồ tổng quát hệ thống điều khiển tự động 
Mọi hệ thống điều khiển tự động đều bao gồm 3 bộ phận cơ bản : 
- Thiết bị điều khiển C (Controller device). 
- Đối tượng điều khiển (Object device). 
- Thiết bị đo lường (Measuring device). 
u(t) tín hiệu vào ; e(t) Sại lệch điều khiển ; x(t) Tín hiệu điều khiển ; y(t) Tín 
hiệu ra ; z(t) Tín hiệu phản hồi 
1.3 Các nguyên tắc điều khiển cơ bản 
Có 3 nguyên tắc điều khiển cơ bản : 
 -Nguyên tắc điều khiển theo sai lệch (Hình 1.3). 
OC
M
- 
z(t) 
u(t) e(t) x(t) y(t) 
Hình 1.3: Sơ đồ nguyên tắc điều khiểntheo sai lệch 
Tín hiệu ra y(t) được đưa vào so sánh với tín hiệu vào u(t) nhằm tạo nên tín 
hiệu tác động lên đầu vào bộ điều khiển C nhằm tạo tín hiệu điều khiển đối 
tượng O. 
Giáo trình Lý thuyết điều khiển tự động 1 
-Nguyên tắc điều khiển theo phương pháp bù nhiễu (Hình 1.4) 
 3
 OC
K
u(t) x(t) e(t) 
y1(t) 
y(t) 
Hình 1.4: Sơ đồ nguyên tắc điều khiển bù nhiễu 
Nguyên tắc bù nhiễu là sử dụng thiết bị bù K để giảm ảnh hưởng của nhiễu là 
nguyên nhân trực tiếp gây ra hậu quả cho hệ thống (hình 1.4). 
-Nguyên tắc điều khiển theo sai lệch và bù nhiễu (Hình 1.5) 
O C
K
u(t) y(t) x(t)e(t)
y1(t) 
M
- 
z(t)
Hình 1.5: Sơ đồ nguyên tắc điều khiển hỗn hợp 
Nguyên tắc điều khiển hỗn hợp là phối hợp cả hai nguyên tắc trên, vừa có hồi 
tiếp theo sai lệch vừa dùng các thiết bị để bù nhiễu. 
1.4 Phân loại các hệ thống điều khiển tự động. 
1.4.1 Phân loại theo nguyên lý xây dựng. 
Các phần tử được phân chia thành các loại: hệ thống ĐK theo mạch hở, hệ 
thống ĐK theo mạch kín và hệ thống ĐK hỗn hợp . 
Ngoài những nguyên lý trên, từ những năm 60 của thế kỷ XX, trên cơ sở áp 
dụng điều khiển học trong cơ thể sống vào kỹ thuật đã ra đời một loại hình hệ 
thống tự động mô phỏng hoạt động của cơ thể sống: đó là các hệ tự chỉnh, thích 
nghi. Nguyên lý tự chỉnh và thích nghi không đòi hỏi phải biết đầy đủ các đặc 
tính của quá trình điều khiển và trong quá trình làm việc, các hệ thống này tự 
chỉnh và thích nghi với các điều kiện bên ngoài thay đổi. 
Lý thuyết các hệ ĐK tự chỉnh và thích nghi đã trở thành một nhánh phát triển 
quan trọng của lý thuyết ĐKTĐ. 
Giáo trình Lý thuyết điều khiển tự động 1 
Vì hầu hết các hệ thống ĐKTĐ trong kỹ thuật là những hệ mạch kín và quá 
trình điều khiển các thiết bị kỹ thuật chung quy lại là quá trình điều chỉnh các 
tham số của nó, nếu dưới đây chúng ta sẽ đề cập đến sự phân loại các hệ thống 
ĐKTĐ mạch kín và lý thuyết về các hệ đó. 
1.4.2/ Phân loại theo tính chất của lượng vào. 
Tuỳ theo tính chất của tác động đầu vào, các hệ thống ĐKTĐ có 3 loại: 
Hệ thống ổn định tự động (điều chỉnh theo hằng số) là hệ thống có lượng vào 
không đổi. Nhiệm vụ của hệ thống là duy trì một hoặc một vài đại lượng vật lý ở 
giá trị không đổi. Thí dụ như hệ thống ĐKTĐ tốc độ động cơ nhiệt, hệ thống 
ĐKTĐ điện áp, tần số của máy phát, hệ ổn định đường bay của máy bay khi góc 
lái không thay đổi ... 
Hệ thống điều chỉnh theo chương trình là hệ thống có lượng vào là các hàm 
đã biết trước, có thể dưới dạng chương trình.Thí dụ hệ điều khiển đường bay 
định trước của máy bay không người lái, hệ thống điều khiển các máy công cụ: 
bào, phay với chương trình định trước trong bộ nhớ máy tính... 
Hệ tự động bám, gọi tắt là hệ bám là hệ thống có lượng vào là các hàm thời 
gian không biết trước, có thể thay đổi theo quy luật bất kỳ. Nhiệm vụ của hệ là 
bảo đảm lượng ra phải "bám" theo sự thay đổi của lượng vào. Thí dụ các hệ như 
là hệ bám đồng bộ góc, các hệ bám vô tuyến điện tử của các đài radar... 
1.4.3/ Phân loại theo dạng tín hiệu sử dụng trong hệ thống. 
Theo dạng tín hiệu sử dụng trong hệ thống, chúng ta có các tác động liên tục 
và các hệ thống gián đoạn (hay hệ rời rạc). 
Hệ tác động liên tục (gọi tắt là hệ liên tục) là hệ mà tất cả các phẩn tử của hệ 
có lượng ra là các hàm liên tục theo thời gian. 
Tín hiệu dưới dạng hàm liên tục có thể là tín hiệu một chiều (chưa biến điệu) 
hoặc tín hiệu xoay chiều (đã được biến điệu) tương ứng chúng ta có hệ ĐKTĐ 
một chiều (DC) và hệ thống ĐKTĐ xoay chiều (AC) (thí dụ hệ thống bám đồng 
bộ công suất nhỏ dùng động cơ chấp hành 2 p ha). 
 4
Giáo trình Lý thuyết điều khiển tự động 1 
Hệ tác động gián đoạn (gọi tắt là hệ gián đoạn hay hệ rời rạc) là các hệ có 
chứa ít nhất một phần tử gián đoạn, tức là phần tử có lượng vào là một hàm liên 
tục và lượng ra là một hàm gián đoạn theo thời gian. 
Tuỳ theo tính chất gián đoạn của lượng ra, các hệ gián đoạn có thể phân chia 
thành các loại: hệ thống ĐKTĐ xung, hệ thống ĐKTĐ kiểu rơ le và hệ thống 
ĐKTĐ số. 
Nếu sự gián đoạn của tín hiệu ra xẩy ra qua những thời gian xác định (ta gọi là 
gián đoạn theo thời gian) khi tín hiệu vào thay đổi, thì ta có hệ ĐKTĐ xung. 
Nếu sự gián đoạn của tín hiệu xẩy ra khi tín hiệu vào qua những giá trị ngưỡng 
xác định nào đó (chúng ta gọi là gián đoạn theo mức), thì có thể ĐKTĐ kiểu rơle. 
Hệ rơle thực chất là hệ phi tuyến, vì đặc tính tĩnh của nó là hàm phi tuyến. Đây là 
đối tượng nghiên cứu của một phần quan trọng trong lý thuyêt ĐK . 
Nếu phần tử gián đoạn có tín hiệu ra dưới dạng mã số (gián đoạn cả theo mức 
và cả theo thời gian), thì ta có hệ ĐKTĐ số. Hệ thống ĐKTĐ số là hệ chứa các 
thiết bị số (các bộ biến đổi A/D, D/A, máy tính điện tử (PC), bộ vi xử lý. 
1.4.4/ Phân loại theo dạng phương trình toán học mô tả hệ thống. 
Về mặt toán học, các hệ thống ĐKTĐ đều có thể mô tả bằng các phương trình 
toán học: phương trình tĩnh và phương trình động. Dựa vào tính chất của các 
phương trình, chúng ta phân biệt hệ thống ĐKTĐ tuyến tính và hệ ĐKTĐ không 
tuyến tính (phi tuyến). 
Hệ thống ĐKTĐ tuyến tính là hệ thống được mô tả bằng phương trình toán 
học tuyến tính. Tính chất tuyến tính của các phần tử và của cả hệ thống ĐKTĐ 
chỉ là tính chất lý tưởng. Vì vậy, các phương trình toán học của hệ thống là các 
phương trình đã được tuyến tính hoá, tức là thay các sự phụ thuộc gần đúng 
tuyến tính. 
Hệ tuyến tính có phương trình động học với các tham số không thay đổi thì 
gọi là hệ ĐKTĐ tuyến tính có tham số không thay đổi, hay hệ ĐKTĐ tuyến tính 
dừng, còn nếu hệ thống có phương trình với tham số thay đổi thì gọi là hệ 
ĐKTĐ tuyến tính có tham số biến thiên, hay hệ ĐKTĐ tuyến tính không dừng. 
 5
Giáo trình Lý thuyết điều khiển tự động 1 
Hệ thống ĐKTĐ phi tuyến là hệ thống được mô tả bằng phương trình toán 
học phi tuyến. Hệ phi tuyến là hệ có chứa các phần tử phi tuyến điển hình, thí dụ 
đó là hệ có chứa các phần tử rơle. 
1.4.5/ Phân loại theo tính chất của các tác động bên ngoài. 
Các tác động bên ngoài vào hệ tự động có quy luật thay đổi đã biết trước hoặc 
mang tính chất ngẫu nhiên. 
Hệ thống tiền định là các hệ có các tác động bên ngoài là tiền định, tức là đã 
biết trước các quy luật thay đổi của nó (thí dụ xét hệ thống với các tác động điển 
hình). 
Hệ thống không tiền định (hay hệ ngẫu nhiên) là các hệ được xem xét nghiên 
cứu khi các tác động bên ngoài là các tín hiệu ngẫu nhiên. 
1.4.6/ Phân loại theo số lượng đại lượng cần điều khiển. 
Tuỳ theo số lượng cần điều khiển (lượng ra của hệ) chúng ta có: hệ một chiều 
và hệ nhiều chiều. 
Hệ thống ĐKTĐ một chiều có chứa một đại lượng cần điều khiển, còn hệ 
ĐKTĐ nhiều chiều là hệ có chứa từ hai đại lượng cần điều khiển trở lên. Thí dụ 
về hệ nhiều chiều có thể là hệ thống ĐKTĐ một máy phát điện, nếu hệ thống 
ĐKTĐ cùng một lúc điều khiển tự động điện áp và tần số của nó. 
Ngoài các cách phân loại chính đã xét ở trên, tuỳ thuộc vào sự tồn tại sai số 
của hệ ở trạng thái cân bằng, chúng ta phân biệt hai loại hệ thống: hệ thống tĩnh 
(có sai số tĩnh) và hệ phiếm tĩnh (không có sai số tĩnh). Tuỳ thuộc vào quy luật 
(định luật) điều khiển (tức là dạng của tín hiệu điều khiển x(t) do cơ cấu điều 
khiển tạo ra), chúng ta phân biệt các bộ điều khiển tỷ lệ (bộ điều khiển P), bộ 
điều khiển tỷ lệ vi phân (bộ điều khiển PD), bộ điều khiển vi phân - tích phân 
(bộ điều khiển PID). 
1.5 Quá trình thiết lập một hệ thống điều khiển 
- Bước 1: Chuyển đổi các yêu cầu kỹ thuật thành một hệ thống vật lý. 
- Bước 2: Vẽ sơ đồ khối chức năng. Chuyển đổi sự miêu tả đặc tính hệ 
thống thành một sơ đồ khối chức năng. Đây là sự miêu tả về các phần 
chi tiết của hệ thống và mối quan hệ giữa chúng. 
 6
Giáo trình Lý thuyết điều khiển tự động 1 
- Bước 3: Thiết lập sơ đồ nguyên lí. 
- Bước 4: Sử dụng sơ đồ nguyên lý thiết lập sơ đồ khối hoặc graph tín 
hiệu hoặc biểu diễn không gian trạng thái. 
- Bước 5: Rút gọn sơ đồ khối. 
- Bước 6: Phân tích và thiết kế. 
 7
Giáo trình Lý thuyết điều khiển tự động 1 
Câu hỏi ôn tập chương 1 
1. Hệ thống điều khiển tự động có thể phân loại như thế nào?
2. Hệ thống điều khiển có mấy phần tử cơ bản? 
3. Hãy nêu các quy tắc điều khiển cở bản để điều khiển một hệ thống điều 
khiển? 
4. Nêu các bước thiết lập một hệ thống điều khiển? 
 8
Giáo trình Lý thuyết điều khiển tự động 1 
CHƯƠNG 2: MÔ HÌNH TOÁN HỌC CỦA HỆ THỐNG ĐIỀU KHIỂN 
Mỗi hệ thống có thể chia làm nhiều phần sẽ thuận tiện hơn và mỗi phần 
sẽ được biễu diễn bằng 1 hàm toán học gọi là hàm truyền đạt (transfer 
function) 
Hệ thống 
(System) 
Đầu ra Đầu vào
Hình 2.1 : Sơ đồ phân chia hệ một hệ thống điều khiển thành các hệ thống 
Hệ thống con 
(subsystem) 
Hệ thống con
(subsystem)
ố
Hệ thống con 
(subsystem) 
Đầu ra Đầu vào 
ố
2.1 Các khâu cơ bản 
Ta có một hệ thống điều khiển: 
 9
Hình 2.2 : Sơ đồ một hệ thống điều khiển tổng quát 
Bộ điều 
khiển 
± 
C1
E 
Đo 
lường 
Đối 
tượng 
Chấp 
hành 
CR 
Đa phần các mạch phản hồi của hệ thống điều khiển là mạch phản hồi âm. 
Khi chúng ta tiến hành phân tích hệ thống tốt hay xấu hay thiết kế bộ điều khiển 
cho hệ thống đều phải xuất phát từ mô hình toán học của hệ thống hay nói cách 
khác ta phải tìm được quan hệ giữa đầu vào và đầu ra của hệ thống. 
2.1.1 Khâu khuếch đại 
x y 
K
Hình 2.3 : Sơ đồ khâu khuếch đại tĩnh 
- Khâu khuếch đại là tín hiệu đầu ra là khuếch đại của tín hiệu đầu vào 
y = K.x (2.1) 
trong đó: K là hệ số khuếch đại 
( Khuếch đại tĩnh là cứ có tín hiệu đầu vào thì tìm được tín hiệu đầu ra) 
Giáo trình Lý thuyết điều khiển tự động 1 
- Cũng có hệ thống có khuếch đại nhiều tầng 
 10
x y 
K1 K2 K3 
Hình 2.4: Sơ đồ khâu khuếch đại tầng 
2.1.2 Khâu tích phân 
)()(1)(
0
0∫ += t
ti
ydttx
T
ty (2.2) 
Với Ti là thời gian tích phân 
2.1.3 Khâu vi phân 
dt
dxTy D= (2.3) 
TD là hằng số thời gian vi phân 
2.1.4 Khâu bậc nhất 
 xKy
dt
dyT .=+ (2.4)
trong đó: K là hệ số truyền của khâu 
 T là hằng số thời gian của khâu 
Phản ứng của hệ thống tốt hay xấu phụ thuộc vào hệ số K, nhanh hay chậm phụ 
thuộc vào T. 
2.1.5 Khâu bậc hai 
)()(22 tKxty
dt
dyT
dt
dyT =++ ζ (2.5)
Trong đó: K là hệ số khuếch đại 
 T là hằng số thời gian 
 ξ độ suy giảm tín hiệu 
Đây là mô hình toán học của mạch RLC. 
2.1.6 Khâu bậc n 
)(...)(... 11
1
1011
1
10 txbdt
xdb
dt
xdb
dt
xdbtya
dt
yda
dt
yda
dt
yda mmm
m
m
m
nnn
n
n
n
++++=++++ −−
−
−−
−
 (2.6) 
thông thường n≥m. 
2.2 Mô hình trong miền tần sô 
2.2.1 Khái niệm về phép biến đổi Laplace và ứng dụng 
Giáo trình Lý thuyết điều khiển tự động 1 
2.2.1.1 Khái niệm và bản chất của phép biến đổi Laplace : 
 Khi sử dụng các phép biến đổi tín hiệu hệ thống từ miền thời gian sang miền 
khác để thuận tiện trong việc xử lý tín hiệu. Như trong hệ thống liên tục người ta 
hay sử dụng phép biến đổi Lpalace để biến đổi từ miền thời gian sang miền tần 
số phức. Các phương trình vi tích phân sẽ chuyển đổi thành các phương trình đại 
số thông thường. 
Trong các hệ thống rời rạc người ta hay sử dụng phép biến đổi Z để chuyển 
tín hiệu tự miền thời gian sang miền tần số phức. Trong thực tế người ta còn sử 
dụng các phép biến đổi khác để xử lý tín hiệu như giải tương quan, mã hoá có 
hiệu quả, chống nhiễu,. 
Thực hiện các phép biến đổi có công cụ toán học như máy tính số, công cụ 
phổ biến và hiệu quả là phần mềm Matlab hay thực hiện biến đổi bằng tay. 
a) Biến đổi Laplace thuận 
Định nghĩa: Gọi F(s) là biến đổi Laplace của hàm f(t), khi đó ta có: 
∫∞ −==
0
)()]([)( dtetftfsF stL (2.7) 
trong đó: 
- ωσ js += 
- là hạt nhân của phép biến đổi. ste−
- F(s) là hàm phức. 
- f(t) là hàm biểu diễn trên miền thời gian xác định trên R. 
Để thực hiện được biến đổi Laplace hàm f(t) phải là hàm thực và thoả mãn 
một số điều kiện sau: 
- f(t) là hàm gốc khi thoả mãn các điều kiện sau: 
 1. f(t) = 0 khi t < 0 
 2. f(t) liên tục khi t≥0, trong khoảng hữu hạn bất kỳ cho trước chỉ có hữu hạn 
các đỉêm cực trị. 
 3. Hàm f(t) gọi là hàm bậc số mũ khi t → ∞ nếu tồn tại một số thực α ≥ 0 và 
M >0 thì 0,)( >∀≤ tMetf tα , α được gọi là chỉ số tăng của hàm f(t). Khi đó 
hàm f(t) là hàm bậc số mũ nếu hàm f(t) tăng không nhanh hơn hơn hàm et. 
- Nếu f(t) là hàm gốc có chỉ số tăng α thì tích phân sẽ hội tụ 
trong miền Re(s) = σ > α. Khi đó sẽ là một hàm phức. 
∫+∞ −=
0
)( dttfeI st
)()(
0
sFdttfeI st == ∫+∞ −
 11
Giáo trình Lý thuyết điều khiển tự động 1 
Ví dụ 1: Tìm ảnh của hàm gốc sau 
f(t)
⎪⎩
⎪⎨
⎧
≥
<≤−
<≤
=
 3 tkhi 0
3t2 khi 1
2t0 khi 1
)(tf
1
0
1 2 3 4 5 t
-1
Áp dụng công thức biến đổi ta có 
)21(111)()()()( 32
3
2
2
0
3
2
2
00
ppststststst ee
s
e
s
e
s
dttfedttfedttfesF −−−−−−
∞+
− +−=+−=−== ∫∫∫
Ví dụ 2: Cho hàm 
1
0
⎩⎨
⎧
<
≥=
0 tkhi0
0 tkhi1
)(tf
f(t)
t 
Tìm biến đổi Laplace? 
Giải 
ss
edttfesF
st
st 1)()(
00
=−==
+∞−∞+
−∫ 
Ví du 3: Tìm ảnh Laplace của hàm f(t) = 4t2 
Từ bảng biến đổi Laplace ta có 
Áp dụng biến đổi tìm ảnh Laplace của hàm f(t) = 4t2 
b) Biến đổi Laplace ngược: 
Biến đổi Laplace ngược là xác định tín hiệu f(t) từ ảnh Laplace F(s) của nó. 
Gọi f(t) là gốc của ảnh F(s) Khi đó ta có: 
∫
∞+
∞−
− ==
jc
jc
st dsesF
j
tfsFL )(
2
 ... t ra thì ta sẽ chọn cấu trúc PID 
7.3 Điều khiển được và quan sát được 
Cho hệ thống có mô hình trạng thái như sau: 
uDxCy
uBxAx
+=
+=&
Hệ thống được gọi là điều khiển được nếu và chỉ nếu tồn tại tín hiệu điều 
khiển u có thể đưa hệ từ trạng thái ban đầu x(0) tới trạng thái x(T) trong một 
khoảng thời gian hữu hạn T. 
Hệ thống là điều khiển được nếu và chỉ nếu ma trận P = [B AB A2B ...An-1B] 
có hạng bằng n hay ma trận P không suy biến. 
Hệ thống được gọi là quan sát được nếu biến trạng thái x(0) được xác định 
khi biết được u và y trong thời gian hữu hạn 0 < t < T. 
Hệ thống là quan sát được nếu và chỉ nếu ma trận Q = [CT ATCT ... (AT)n-1CT] 
có hạng bằng n hay định thức của Q khác không. 
 130
Giáo trình Lý thuyết điều khiển tự động 1 
Câu hỏi ôn tập chương 7 
1. Tổng hợp bộ điều khiển là gì? 
2. Có mấy cách phân loại bộ điều khiển? Nêu chi tiết các cách đó. 
3. Nêu cách tổng hợp bộ điều khiển theo phương pháp Ziegler-Nichols. 
4. Tại sao phải xét tính điều khiển được và quan sát được? 
 131
Giáo trình Lý thuyết điều khiển tự động 1 
CHƯƠNG 8: HỆ THỐNG ĐIỀU KHIỂN SỐ 
8.1 Mở đầu 
 Máy tính có thể hoạt động như một bộ bù hay bộ điều khiển trong hệ thống 
điều khiển phản hồi. Các quá trình và hệ thống có sử dụng máy tính số, có bộ 
điều khiển, có thiết bị biến đổi xung đều thuộc hệ lớp hệ thống xung số. Máy 
tính chỉ nhận dữ liệu tại m ng thời gian nhất định.Việc phát triển phương 
pháp để miêu tả và phân t
là rất cần thiết. 
 thống máy tính sử
x , kết quả là t
m thể biến đổi từ m
trong miền tần số phức cũ
 Ta sử dụng hàm truyền
thời của hệ thống. Vì vậy
điều khiển có phản hồi củ
điều khiển. Hệ thống điều
Máy tính 
số 
(digit
đ
(digital
(digital
Tín hiệu 
điều
Hình 8.1: Sơ đ
 ột khoảích sự hoạt động của hệ thống điều khiển có máy tính 
 dụng dữ liệu trích mẫu trong khoảng thời gian 
u được lấy m ên tục. Các tín hiệu đã được trích 
iền s sang miền z theo mối quan hệ z = e sT. Biến z ác định
ẫu có Hệ ín hiệng có các tính 
 có biến đổi z
 chúng ta có th
a máy tính số 
 khiển có sử du
al Bộ biến 
đổi D/A 
(
Bộ biến 
ổi A/D 
(ana
ồ điều khiển p
13được 
ẫu lichất tương tự như trong miền s Laplace. 
 để phân tích sự ổn định và đáp ứng tức 
ể xác định được đáp ứng của hệ thống 
mà hoạt động như là một bộ bù hay bộ 
ng máy tính số như sau: 
analog Cơ cấu chấp 
hành 
Quá trình 
công nghệ
Đo lường
log)
hản hổi có sử dụng máy tính 
2
Giáo trình Lý thuyết điều khiển tự động 1 
Ngày nay máy tính số được sử dụng rộng rãi trong công nghiệp nó giữ một 
vai trò quan trong trong quá trình công nghiệp, máy tính được sử dụng với cơ 
cấp chấp hành để thực hiện các nhiệm vụ điều khiển. 
 Máy tính không được nối trực tiếp với cơ cấu chấp hành hay các quá trình 
mà qua bộ biến đổi số tương tự(Digital/Analog Converter). Chúng ta đã biết tất 
cả các con số truyền vào máy tính hay đi truyền ra đều được thực hiện trong một 
khoảng thời gian thời gian cố định và bằng nhau, T được gọi là chu kỳ lấy mẫu. 
Vì vậy tín hiệu chủ đạo sẽ có dạng là r(kT). Các biến r(kT), m(kT) và u(kT) là 
các tín hiệu rời rạc. 
Bộ lấy mẫu lý tưởng là 
Bộ trích mẫu 
r(t) r*(t) 
Tín hiệu liên tục Tín hiệu trích mẫu 
Máy tính 
số 
Bộ biến 
đổi D/A 
Cơ cấu 
chấp hành 
Quá trình 
công nghệ
Bộ biến 
đổi A/D 
Đo lường
u(t) 
p(t) m(kT) 
u(kT)
r(kT) 
Tín hiệu 
điều
Hình 8.2: Tín hiệu được trích mẫu sử dụng trong máy tính số 
Tín hiệu ra là r*(t), tại nT là thời gian lấy mẫu hiện thời và giá trị r*(t) là r(nT), 
tổng quát tín hiệu ra là 
r*(nT) = r(nT)δ(t-nT) (8.1) 
 133
Giáo trình Lý thuyết điều khiển tự động 1 
r(4T)
r(3T) 
r(2T) 
r(T)
r(t) 
r(kT)
0
t kT
 2T 3T 4T T 2T 3T 4T 0 T 
Hình 8.3: Tín hiệu r(t) được trích mẫu 
Tín hiệu không liên tục mà ta quan tâm ở đây là dãy các giá trị {rk} cách đều 
nhau với rk = r(kT),trong đó T được gọi là chu kỳ trích mẫu ( hay là chu kỳ 
lượng tử hoá ). Đây là loại tín hiệu chỉ có giá trị tại những điểm {t=kT} k là các 
số nguyên , và ngoài các điểm này thì không được định nghĩa . Nếu mỗi giá trị rk 
được xem như tích r(t)δ(t-T ) thì toàn bộ dãy {rk} sẽ là : 
Lúc này {rk} gọi là tín hiệu xung . 
( )
 )()(
)()()()()()(
∑
∑∑
∞
−∞=
∞
−∞=
∞
−∞=
−=
=−=−=
k
kk
k
kTtts
tstrkTttrkTttrr
δ
δδ
 (8.2) 
Để hiểu rõ hơn ta xem mô hình trích mẫu như sau 
134
Giáo trình Lý thuyết điều khiển tự động 1 
Hình 8.4: Tích của dạng sóng theo thời gian và tín hiệu trích mẫu 
f(t) là dạng sóng liên tục, s(t) là hàm mẫu có độ rộng xung bằng nhau và bằng 
Tw (có biên độ là một hằng số), f*Tw(t) là tín hiệu đầu ra. 
∑∞
−∞=
−−−−==
k
wT TkTtukTtutftstftf w )()()()()()(
* (8.3) 
k là số nguyên chạy từ - ∞ → +∞, T là chu kỳ trích mẫu, Tw là độ rộng xung. 
Giả sử rằng Tw rất nhỏ so với T, f(t) có thể coi là hằng số trong khoảng thời gian 
trích mẫu và f(t) = f(kT). 
[∑∞
−∞=
−−−−=
k
wT TkTtukTtukTftf w )()()()(
* ] (8.4) 
thực hiện biến đổi Laplace 
kTs
k
sT
k
sTkTskTs
T es
ekTf
s
e
s
ekTfsF
ww
w
−∞
−∞=
−∞
−∞=
−−− ∑∑ ⎥⎦
⎤⎢⎣
⎡ −=⎥⎦
⎤⎢⎣
⎡ −= 1)()()(* (8.5) 
Thay e –Tws đã khai triển 
 135
Giáo trình Lý thuyết điều khiển tự động 1 
( )
kTs
k
w
w
T es
sTsT
kTfsF
w
−∞
−∞=
∑
⎥⎥
⎥⎥
⎥
⎦
⎤
⎢⎢
⎢⎢
⎢
⎣
⎡
⎭⎬
⎫
⎩⎨
⎧ −+−−
=
L
!2
11
)()(
2
* (8.6) 
Vì Tw là bé nên 
kTs
k
w
kTs
k
w
T eTkTfes
sTkTfsF
w
−∞
−∞=
−∞
−∞=
∑∑ =⎥⎦
⎤⎢⎣
⎡= )()()(* (8.7) 
Cuối cùng thực hiện biến đổi về miền thời gian 
)()()(* kTtkTfTtf
k
wTw
−= ∑∞
−∞=
δ (8.8) 
8.2 Mô hình giữ mẫu bậc không 
Bước cuối cùng trong việc xây dựng mô hình của máy tính số là mô hình giữ 
mẫu bậc không. Nếu coi bộ trích mẫu là lý tưởng thì Tw =1 và xét tại thời điểm t 
= 0 và t = T ta có 
Ts
h ess
sG −−= 11)( (8.9) 
 136
Hình 8.5: Tín hiệu r(t) được trích mẫu 
f(t) 
 t 
f*(t)
 T 2T 3T 4T 
f(kT)δ(t-kT) 
 T 2T 3T 0 0 
 0 
t
fh(t) 
fh(t) 
ZOH 
f*(t) f(t) 
Bộ trích mẫu 
lý tưởng 
 4T 3T 2T T 
 4T 
t 
Giáo trình Lý thuyết điều khiển tự động 1 
8.3 Biến đổi Z 
Mục đích của biến đổi z là đưa về hàm trưyền đạt chứa đựng thông tin về hệ 
thống mà ta có thể phân tích và thiết kế được sự ổn định của hệ thống. 
Thực hiện biến đổi Laplce với bộ trích mẫu là lý tưởng 
kTs
k
T ekTfsF w
−∞
=
∑=
0
* )()( (8.10) 
Thay thế z = e – Ts
k
k
zkTfzF −
∞
=
∑=
0
)()( (8.11) 
Ví dụ: xác định hàm truyền z của bộ lấy mẫu sườn dốc 
Đối với tín hiệu có sườn dốc f(kT) = kT 
)()(
0
* kTtkTtf
k
−=∑∞
=
δ (8.12) 
Thực hiện biến đổi Laplace 
kTs
k
ekTsF −
∞
=
∑=
0
* )( (8.13) 
Thực hiện biến đổi z = e – Ts
)32()( 321
00
L+++=== −−−−∞
=
−∞
=
∑∑ zzzTekTekTzF kz
k
kz
k
 (8.14) 
Biến đổi đưa về dạng zF(z) 
)321()( 21 L+++= −− zzTzzF (8.15) 
Lấy công thức (8.15) trừ (8.14) ta được 
)1()()1()()( 21 L+++=−=− −− zzTzFzzFzzF (8.16) 
Mặt khác 
L+++=−
−−
−
21
1
1
1
1 zz
z
 (8.17) 
 137
Giáo trình Lý thuyết điều khiển tự động 1 
Thay (8.17) vào (8.16) 
2)1(
)( −= z
zTzF (8.18) 
Nếu muốn thực hiện phép biến đổi z ngược ta có hai cách: 
- Phân tích thành các phân thức thành phần. 
- Hạ bậc phân thức. 
Ví dụ : Tìm f*(t) của hàm F(z) sau 
)7.0)(5.0(
5.0)( −−= zz
zzF (8.19) 
Thực hiện chia cho z và phân tích thành các phân thức con 
7.0
5.2
5.0
5.2
7.05.0)7.0)(5.0(
5.0)(
−+−
−=−+−=−−= zzz
B
z
A
zzz
zF (8.20) 
hay 
7.0
5.2
5.0
5.2
)7.0)(5.0(
5.0)( −+−
−=−−= z
z
z
z
zz
zzF (8.21) 
Tra ngược lại 
f(kT) = -2.5(0.5)k + 2.5(0.7)k (8.22) 
Tìm dạng sóng f*(t) lý tưởng 
[ )(2.5(0.7)k 2.5(0.5)k -)()()(* kTtkTtkTftf
kk
−+=−= ∑∑ ∞
−∞=
∞
−∞=
δδ ] (8.23) 
Nếu thay k = 0, 1, 2 và 3 ta có 4 số hạng đầu tiên là 
)3(545.0)2(6.0)(5.0)(0)(* TtTtTtttf −+−+−+= δδδδ (8.24) 
Nếu thực hiện bằng cách chia liên tiếp ta có 
 138
Giáo trình Lý thuyết điều khiển tự động 1 
21.0545.0
21.0720.06.0
175.06.0
175.06.05.0
5.035.02.1
545.06.05.0
1
1
1
1
2
321
−
+−
−
+−
+−
++
−
−
−
−
−−−
z
z
z
zz
zzz
zzz
 (8.25) 
Sử dụng tử số và định nghĩa z 
L+++= −−− TsTsTs eeesF 32* 545.06.05.0)( (8.26) 
Từ miền thời gian 
L+−+−+−= )3(545.0)2(6.0)(5.0)(* TtTtTttf δδδ (8.27) 
8.4 Hàm truyền đạt 
Ta có dạng của tín hiệu 
)()()( kTtkTftf
k
−= ∑∞
−∞=
δ (8.28) 
Tín hiệu trích mẫu đầu vào là 
)()()(
0
* nTtnTftr
n
−=∑∞
=
δ (8.29) 
G(s)
C(s) R(s) 
R*(s)
R*(s)
G(s)
C(s) C*(t) R(s) 
G(s)
C(s) R(s) 
Hình 8.6: Hệ thống tín hiệu trích mẫu 
Đáp ứng xung của hệ thống G(s) là g(t), tín hiệu ra của G(s) có thể được viết 
bằng tổng các xung được tạo ra khi cho tín hiệu tác động ở đầu vào. 
 139
Giáo trình Lý thuyết điều khiển tự động 1 
)()()(
0
nTtgnTrtc
n
−=∑∞
=
 (8.30) 
Sử dụng công thức 8.11 ta có 
k
k
zkTczC −
∞
=
∑=
0
)()( (8.31) 
Sử dụng công thức 8.30 với t = kT 
)()()(
0
nTkTgnTrkTc
n
−=∑∞
=
 (8.32) 
Thay công thức 8.32 vào công thức 8.31 ta được 
 140
][ k
k n
zTnkgnTrzC −
∞
=
∞
=
∑∑ −=
0 0
)()()( (8.33) 
Đặt m = k – n 
[ ]
[ ] [ ] ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧=
=
−∞
=
−∞
=
+−∞
=+
∞
=
∑∑
∑ ∑
n
n
m
m
nm
nm n
zmTgnTrzmTg
zmTgnTrzC
00
)(
0 0
)(
)()(
 (8.34) 
Tại giới hạn dưới m + n → m. Mặt khác m + n = 0 khi m 0. Nhưng 
khi m < 0 thì g(mT) = 0, m không nhỏ hơn 0. Bên cạnh đó g(t) = 0 khi t < 0. 
Áp dụng định nghĩa biến đổi z ta có 
[ ] [ ] )()()()(
00
zRzGzmTgnTrzmTgzC n
n
m
m
=⎭⎬
⎫
⎩⎨
⎧
⎭⎬
⎫
⎩⎨
⎧= −∞
=
−∞
=
∑∑ (8.35) 
Ví dụ: Ta có khâu giữ mẫu bậc không ghép nối tầng với 
1
21)(hay 
1
2)(1 +
+⎟⎠
⎞⎜⎝
⎛ −=+
+=
−
s
s
s
esG
s
ssG
Ts
 (8.36) 
Tìm hàm truyền G(z) nếu như chu kỳ trích mẫu là 0.5s 
Giải 
Vì khâu z.0.h được mắc nối tầng với G1(s) nên ta có thể viết như sau 
Giáo trình Lý thuyết điều khiển tự động 1 
( ) )(1)( 1
s
sGesG Ts−−= (8.37) 
từ 
⎭⎬
⎫
⎩⎨
⎧−=⎭⎬
⎫
⎩⎨
⎧−= −
s
sGz
z
z
s
sGzzzG )(1)()1()( 111 (8.38) 
Thực hiện biến đổi Laplace ngược 
1
12
1)1(
2)()( 12 ++=++=+
+==
sss
B
s
A
ss
s
s
sGsG (8.39) 
Biến đổi Laplace ngược 
tetg −−= 2)(2 (8.40) 
và khi t = kT 
kTekTg −−= 2)(2 (8.41) 
Tra bảng ta tìm được G2(z) 
Tez
z
z
zzG −−−−= 1
2)(2 (8.42) 
Thay T = 0.5 vào 8.42 
)607.0)(1(
214.0
607.01
2)()(
2
1
2 −−
−=−−−=⎭⎬
⎫
⎩⎨
⎧=
zz
zz
z
z
z
z
s
sGzG (8.43) 
Thay vào 8.38 ta tìm được G(z) 
607.0
214.0)(1)( 2 −
−=−=
z
zsG
z
zzG (8.44) 
8.5 Sự ổn định 
Sự khác nhau về sự ổn định giữa hệ thống điều khiển phản hồi tương tự và số 
như sau 
 141
Giáo trình Lý thuyết điều khiển tự động 1 
142
Hình 8.7: Mặt phẳng phân bố sự ổn định 
Trong mặt phảng phức s thì miền ổn định nằm bên trái trục ảo. Hệ thống có 
hàm truyền G(s) được chuyển sang miền gián đoạn là G(z), miền ổn định được 
xác định như sau: 
z = esT = e(σ + jω)T = e σTےωT (8.45) 
trong đó s = σ + jω 
Ở bên trái mặt phẳng phức s, σ <0 tương ứng với 0 < z < 1 thì hệ thống ổn định. 
Ví dụ: cho hệ thống sau 
Hình 8.8: Hệ thống điều khiển phản hồi đã được trích mẫu 
Với T = 1 và 
)1(
)( += ss
KsGp (8.46) 
Thực hiện biến đổi z ta có 
azaz
bazK
zz
zKzG ++−
+=+−
+=
)1(
)(
3678.03678.1
)2644.03678.0()( 22 (8.47) 
e*(t)
G0(s)
r(t) c(t) 
Gp(s)
Im 
Mặt phẳng z
Re
Im 
A
C 
B 
Mặt phẳng s
B 
C ReA
Giáo trình Lý thuyết điều khiển tự động 1 
Với a = 0.3678 và b = 0.2644 
Điểm cực của hệ thống kín là nghiệm của phương trình q(z) = 1 + G(z) = 0 
q(z) = 1 + G(z) = z2 – (1-a)z + a + Kaz + Kb = 0 (8.48) 
Khi K = 1 
 q(z) = z2 – z + 0.6322 
 = (z – 0.50 + j0.6182)(z – 0.50-j0.6182) = 0 (8.49) 
Hệ thống ổn định vì các nghiệm đều nằm trong đường tròn đơn vị. 
Khi K = 10 
 q(z) = z2 + 2.310z + 3.012 
 = (z + 1.155 + j1.295)(z + 
Hệ thống không ổn định vì các nghiệm nằ
Với 0 < K < 2.39 thì hệ thống ổn định. 
8.6 Sai số xác lập 
Chúng ta xem sự ảnh hưởng của việc
thống số. Để đưa ra được các kết luận tổ
vì vị trí trích mẫu có thể làm thay đổi hàm
ta giả thiết vị trí của bộ trích mẫu nằm sau
E*(sR(s) 
s
e−1
T 
Hình 8.9: Sai số xác lập
Sai số trích mẫu là E*(s) = E(z) 
Từ sơ đồ ta có 
 143
 1.155 – j1.295) = 0 (8.50) 
m ở bên ngoài đường tròn đơn vị. 
 trích mẫu đến sai số xác lập trong hệ 
ng quát về sai số xác lập là rất khó bởi 
 truyền đạt của hệ hở. Trong phần này 
 tín hiệu sai lệch. 
C(s) 
Gp(s) Ts−
 của hệ điều khiển số 
Giáo trình Lý thuyết điều khiển tự động 1 
)(1
)()( 
)()()()(
zG
zRzEhay
zGzEzRzE
+=
−=
 (8.51) 
Và áp dụng định lý về giá trị xác lập 
)(1
)()1(lim)()1(lim)( 1
1
1
1
*
zG
zRzzEze
zz +−=−=∞
−
→
−
→ (8.52) 
Nếu tín hiệu vào là tín hiệu bậc thang đơn vị 
1
)( −= z
zzR (8.53) 
Thay R(z) vào 
)(lim1
1)(
1
*
zG
e
z→+
=∞ (8.54) 
Lúc đó hằng số sai số tính là 
)(lim
1
zGK
zp →= (8.56) 
Viết lại theo Kp 
pK
e +=∞ 1
1)(* (8.57) 
Nếu tín hiệu vào là tín hiệu có sườn dốc thì 
2)1(
)( −= z
TzzR (8.58) 
Sai số là 
 1)(
vK
e =∞ (8.59) 
trong đó )()1(lim1
1
zGz
T
K
zv
−= → (8.60) 
Nếu tín hiệu vào là đường Parabol 
 144
Giáo trình Lý thuyết điều khiển tự động 1 
3
2
)1(2
)1()( −
+=
z
zzTzR (8.61) 
Sai số là 
 1)(
aK
e =∞ (8.62) 
trong đó )()1(lim1 2
12
zGz
T
K
za
−= → (8.63) 
Ví dụ: tìm sai số xác lập của hệ thống khi 
)1(
10)( += sssGp (8.64) 
Giải 
Đầu tiên tìm G(s) 
⎥⎦
⎤⎢⎣
⎡
++−−=+
−= −
−
1
111)1(10
)1(
)1(10)(
22 sss
e
ss
esG Ts
Ts
 (8.65) 
Thực hiện biến đổi z 
⎥⎦
⎤⎢⎣
⎡
−
−+−−=
⎥⎦
⎤⎢⎣
⎡
−+−−−−=
−
−
−
T
T
ez
z
z
Tz
ez
z
z
z
z
TzzzG
11
1
10
)1()1(
)1(10)( 2
1
 (8.66) 
Đối với tín hiệu bậc thang đơn vị 
∞== → )(lim1 zGK zp 01
1)(* =+=∞ pK
e (8.67) 
Đối với tín hiệu sườn dốc 
10)()1(lim1
1
=−= → zGzTK zv 0.1
1)( ==∞
vK
e (8.68) 
Đối với tín hiệu Parabol 
 145
Giáo trình Lý thuyết điều khiển tự động 1 
0)()1(lim1 2
12
=−= → zGzTK za 
1)( ∞==∞
aK
e (8.69) 
 146
Giáo trình Lý thuyết điều khiển tự động 1 
Bài tập chương 8 
1. Tìm f(kT) của các hàm truyền z sau: 
a, 
)7.0)(5.0(
)1()( −−
+=
zz
zzzF b, 
)7.0)(5.0(
)2)(1()( −−
++=
zzz
zzzF 
2. Tìm hàm truyền G(z) từ các hàm truyền trong miền phức G(s) với T = 
0.5s 
a, 
)3)(1(
5)( ++
+=
ss
ssG b, 
)4)(3(
)2)(1()( ++
++=
ss
sssG 
c, 
1
2)( +
+=
s
ssG d, 
)134)(2(
30)( 2 +++= ssssG 
3. Tìm hàm truyền G(z) của các hệ thống sau: 
4. Tìm K để hệ thống sau là ổn định. 
5.Tìm hằng số sai số tĩnh sse của hệ thống sau 
Nếu tín hiệu đầu vào là 
a, )(tu
b, )(ttu
c, )(
2
1 2 tut 
 147
Giáo trình Lý thuyết điều khiển tự động 1 
Tài liệu tham khảo 
[1] Norman S.Nise, Control System Engineering, Addision-Wesley 
Publishing Company, 1995. 
[2] Richard C.Dorf, Robert H.Bishop, Modern Control System, Tenth 
Edition, Pearson Prentice Hall, 2005. 
[3] Nguyễn Doãn Phước, Lý thuyết điều khiển tuyến tính, Nhà xuất bản 
Khoa học và kỹ thuật, 2004. 
[4] Phạm Công Ngô, Lý thuyết điều khiển tự động, Nhà xuất bản Khoa học 
và kỹ thuật, 2006. 
[5] Nguyễn Phương, Nguyễn Thị Phương Giang, Cơ sỏ tự động hoá sử dụng 
trong ngành cơ khí, Nhà xuất bản Khoa học và kỹ thuật, 2005. 
[6] Nguyễn Hoài Nam, Bài giảng lý thuyết điều khiển tự động, Đại học Kỹ 
thuật công nghiệp Thái Nguyên. 
[7] Lương Thanh Bình, Bài giảng lý thuyết điều khiển tự động, Đại học Sư 
phạm kỹ thuật Vinh. 
 148